遊蕩點

遊蕩點(wandering point)動態系統的一種相點是，由該點出發的相軌經足夠時間後將不再回歸至它的某個鄰域，其形式定義為：對Rⁿ中(或流形M上)的點p，若存在它的鄰域U⊂Rⁿ(或M)和某時間N>0，使對任意t>N，均有φ_t(U)∩U=∅，即由U內出發的軌道均離開U而不返回，則稱點p為遊蕩點，否則稱為非遊蕩點。

基本介紹

• 中文名：遊蕩點
• 外文名：wandering point
• 屬性：動態系統的一種相點
• 所屬學科：數學
• 相關概念：動態系統，不變集等

基本介紹

非遊蕩點指其任意鄰域具有域回歸性的點，設是上的流(離散動力系統)，若對於的任意鄰域及任意，存在，使得

則點稱為非遊蕩點，對於半流與離散半動力系統，非遊蕩點定義相同。極限點、周期點以及P式穩定軌道上的點都是非遊蕩點，不是非遊蕩點的點稱為遊蕩點。

相關介紹

非遊蕩集是與不變集非常相近似的集合，設點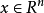，若的任意鄰域U，都存在，當時，則稱是的非遊蕩點，所有非遊蕩點組成的集合為非遊蕩集。

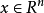
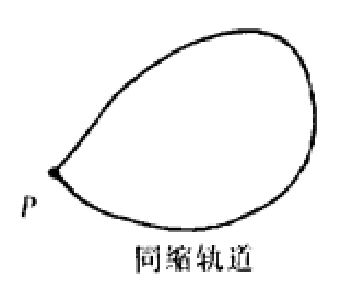圖1

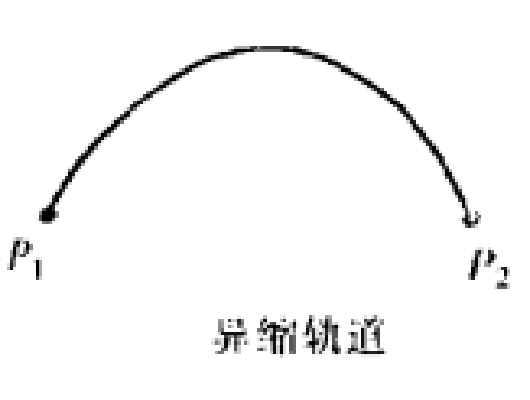圖2

關於非遊蕩集我們有以下結論：上連續動力系統的非遊蕩集(Andronov，et al，1966)只可能有下列三種集合構成：i)的不動點；ii)的周期軌道；iii)的同縮軌道和異縮軌道，而且容易知道若有同縮或異縮軌道為非遊蕩集的一部分時，其上的平衡點若是雙曲的那必是鞍點，因為在匯和源的鄰近不可能有非遊蕩點。若可逆時，非遊蕩點集是不變集。表1給出了上連續的動力系統的非遊蕩集的組成情形。

由表1可見，非遊蕩集由數個互不相交的部分組成，若這些組成部分是連通的，即不能再分解成數個互不相交的組成部分，則可稱其為拓撲可遷的，即非遊蕩集是數個互不相交的拓撲可遷集之並，其嚴格的數學定義如下：

令，是上的動力系統，稱為拓撲可遷的(topological transitive)，若存在單個軌道在A中稠密，即此軌道的閉包為A，且A是的不變集。