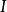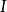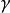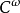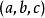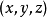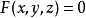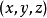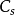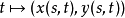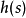基本介紹
- 中文名:漸屈線
- 外文名:Evolute
- 領域:數學
- 適用領域:微分幾何
曲線的微分幾何,概述,定義,法線,法線的計算,法線的唯一性,包絡線,漸伸線,概述,參數化曲線,
曲線的微分幾何
概述
從古代開始,許多具體曲線已經用綜合方法深入研究。微分幾何採取另外一種方式:把曲線表示為參數形式,將它們的幾何性質和各種量,比如曲率和弧長,用向量分析表示為導數和積分。分析曲線最重要的工具之一為Frenet 標架,是一個活動標架,在曲線每一點附近給出“最合適”的坐標系。
曲線的理論比曲面理論及其高維推廣的範圍要狹窄得多,也簡單得多。因為歐幾里得空間中的正則曲線沒有內蘊幾何。任何正則曲線可以用弧長(“自然參數”)參數化,從曲線上來看不能知道周圍空間的任何信息,所有曲線都是一樣的。不同空間曲線只是由它們的彎曲和扭曲程度區分。數量上,這由微分幾何不變數曲線的“曲率”和“撓率”來衡量。曲線基本定理斷言這些不變數的信息完全確定了曲線。
定義
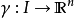
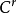


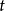


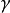


如果I是閉區間 [a,b],我們稱 γ(a) 為曲線 γ 的起點而 γ(b) 為終點。
如果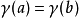 ,我們說 γ 是閉的或是一個環路。進一步,我們稱 γ 是一條閉 C-曲線,如果 γ(a) = γ(b) 對所有k≤r。
,我們說 γ 是閉的或是一個環路。進一步,我們稱 γ 是一條閉 C-曲線,如果 γ(a) = γ(b) 對所有k≤r。
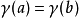
如果 為單射,我們稱為簡單曲線。
為單射,我們稱為簡單曲線。

一條 -曲線
-曲線

特別地,一條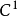 -曲線
-曲線 是正則的如果
是正則的如果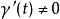 對任何
對任何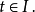
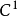

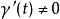
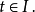
法線
法線是與多邊形(polygon)的曲面垂直的理論線,一個平面(plane)存在無限個法向量(normal vector)。在電腦圖學(computer graphics)的領域裡,法線決定著曲面與光源(light source)的濃淡處理(Flat Shading),對於每個點光源位置,其亮度取決於曲面法線的方向。
法線的計算
法線的唯一性
曲面法線的法向不具有唯一性(uniqueness),在相反方向的法線也是曲面法線。曲面在三維的邊界(topological boundary)內可以分區出inward-pointing normal 與 outer-pointing normal, 有助於定義出法線唯一方法(unique way)。定向曲面的法線通常按照右手定則來確定。
包絡線
漸伸線
概述
漸伸線(involute)(或稱漸開線(evolent))和漸屈線(evolute)是曲線的微分幾何上互為表里的概念。若曲線A是曲線B的漸伸線,曲線B是曲線A的漸屈線。
在曲線上選一定點S。有一動點P由S出發沿曲線移動,選在P的切線上的Q,使得曲線長SP和直線段長PQ相同。漸伸線就是Q的軌跡。
曲線的漸屈線是該曲線每點的曲率中心的集。
若該曲線有參數方程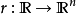 (
(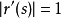 ),則其漸屈線為
),則其漸屈線為
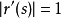

參數化曲線
漸開線方程曲線的參數化定義的函式( x(t) , y(t) )是: