基本介紹
- 中文名:曲線坐標
- 外文名:curvilinear coordinates
- 反算:通過坐標反推里程和偏距
- 正算:通過里程和偏距計算坐標
- 所屬學科:天文學
- 組成:曲線坐標系
曲線坐標系


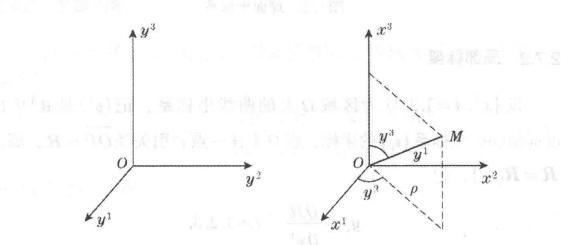 圖1
圖1
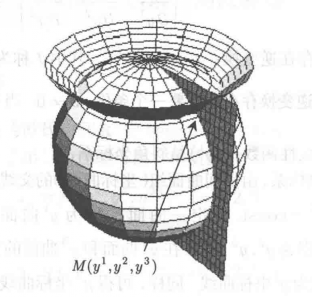 圖2
圖2


 圖1
圖1
 圖2
圖2“曲線坐標”是天文學專有名詞。曲線坐標計算程式可計算圓曲線帶有緩和曲線、邊樁坐標及切線方位角,附有正算、反算功能。正算:通過里程和偏距計算坐標;反算:通過...
曲線坐標計算程式是一款套用軟體,適用PC平台,軟體版本為v1.50.09。...... 曲線坐標計算程式是一款套用軟體,適用PC平台,軟體版本為v1.50.09。軟體名稱 曲線坐標計...
位形坐標曲線(configuration coordinate curves)位形坐標曲線是解釋電子-聲子相互作用的一種物理模型。...
圓橢圓雙曲線拋物線阿基米德螺旋曲線四葉草曲線...... 編輯 數學曲線圓 直角坐標系標準方程:點O(a,b)為圓心,r為半徑,(x-a)^2+(y-b)^2=r^2。極...
分布曲線是以變數值為橫坐標,以累積頻率[機率]為縱坐標的曲線圖,即機率分布函式的圖形。例如正態曲線等。...
伏安特性曲線圖常用縱坐標表示電流I、橫坐標表示電壓U,以此畫出的I-U圖像叫做導體的伏安特性曲線圖。伏安特性曲線是針對導體的,也就是耗電元件,圖像常被用來研究...
維維亞尼曲線(Viviani curve)是一種特殊曲線,球面x²+y²+z²=a²與圓柱面x²+y²-ax=0的交線。它的參數方程可寫作r(t)=(a cos²θ,a cos...
標準曲線(standard curve),數學術語,是指通過測定一系列已知組分的標準物質的某理化性質,從而得到該性質的數值所組成的曲線。標準曲線是標準物質的物理/化學屬性跟...
坐標軸(coordinate axis)用來定義一個坐標系的一組直線或一組線;位於坐標軸上的點的位置由一個坐標值所唯一確定,而其他的坐標軸上的點的位置由一個坐標值所唯一...
曲線,是微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。微分幾何就是利用微積分來研究幾何的學科。為了能夠套用微積分的知識,我們不能考慮...
斯特里貝克(Stribeck)曲線表示了邊界潤滑與流體潤滑的區別。曲線的縱坐標摩擦係數是其橫坐標(潤滑劑粘度×滑動速度)/載荷 )這個變數的函式。而將速度減小,載荷加大,...
粒度分布曲線又稱粒度分布頻率曲線,是在以粒度大小為橫坐標,百分含量為縱坐標的坐標紙上,按各粒級百分含量繪出相應的點後,聯接各粒級百分含量的點即成一波狀起伏...
直觀上,富勒氏曲線可看成空間質點運動的軌跡。曲線的更嚴格的定義是區間【α,b)】到E3中的映射r:【α,b)】→E3。有時也把這映射的像稱為曲線。具體地說,設...
笛卡兒平面直角坐標系中平行於縱坐標軸的方向與某一方向的夾角。坐標方位角是平面直角坐標系中某一直線與坐標主軸(X軸)之間的夾角,從主軸起算,順時針方向自0~360...
曲線,是微分幾何學研究的主要對象之一。直觀上,曲線可看成空間質點運動的軌跡。微分幾何就是利用微積分來研究幾何的學科。為了能夠套用微積分的知識,我們不能考慮...
這種應力-應變曲線通常稱為工程應力-應變曲線,它與載荷-變形曲線相似,只是坐標不同。從此曲線上,可以看出低碳鋼的變形過程有如下特點: 當應力低於σe時,應力與試...
中文名稱 曲線坐標記錄儀 英文名稱 curvilinear coordinate recorder 定義 當傳紙機構靜止而被測量變化時,記錄裝置能給出曲線跡線的記錄儀器。 套用學科 機械工程(...
平行坐標圖是一種通常的可視化方法, 用於對 高維幾何 和 多元數據 的可視化。為了表示在高維空間的一個點集,在N條平行的線的背景下,(一般這N條線都豎直且...
