基本介紹
- 中文名:平方可積函式
- 外文名:square-integrable function
- 學科:數學
- 別稱:二次積分函式
- 可積條件:平方積分為實值或復值可測函式
- 相關名詞:可積函式
定義



性質


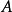
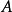
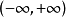


希爾伯特空間
定義
套用
原理






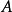
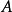
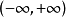
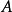
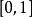



在數學中,平方可積函式是絕對值平方的積分為有限值的實值或復值可測函式,又稱二次積分函式。一個等價的定義是,函式本身的平方(而非它的絕對值)是勒貝格可積的...
數學上,可積函式是存在積分的函式。除非特別指明,一般積分是指勒貝格積分。否則,稱函式為"黎曼可積"(也即黎曼積分存在),或者"Henstock-Kurzweil可積",等等。...
多項式基底是將多項式方程式分解為線性函式。基函式傅立葉基底 正弦和餘弦形成平方可積函式的(正交)Schauder 基。 作為一個特例,該集合為:...
完備系(complete system)是具有某種完備性質的函式系。函式係為完備系的充分必要條件是:任意一個平方可積函式的傅立葉級數均值收斂於它本身。例如:定義在[-π,π...
在數學分析中,以Marc-Antoine Parseval命名的帕塞瓦爾恆等式是一個有關函式的傅立葉級數的可加性的基礎結論。表示可積函式與其傅立葉係數之間關係的恆等式。從幾何...
L2空間是平方可積函式類,它更接近於n維歐氏空間,具有n維歐氏空間許多類似的幾何性質。...
在數學上,一個對偶小波(dual wavelet)為小波的對偶。一般情形下,在里斯表示定理(Riesz representation theorem)中,由平方可積函式(square integral function)產生的...
1965年他證明Lusin猜想成立引起轟動:[0,1]上平方可積函式的Fourier級數幾乎處處收斂。Carleson生平 編輯 Carleson教授1972年證明,在二維情形,任意階的Bochner-Riesz...
§4 平方可積函式§5 高斯積分§6 分部積分法、廣義函式、索伯列夫(Sobolev)空間§7 復積分第五章 傅立葉級數與傅立葉積分§1 傅立葉級數——從什麼是譜談...
在數學中,微分運算元是定義為微分運算之函式的運算元。首先在記號上,將微分考慮為一...在平方可積函式空間中,數量積定義為如果另外增添要求f或g當 等於零,我們也可...
但這兩個可積函式都不是平方可積的。因此盧津猜想不能被否定。從肯定方面來接近盧津猜想的,則有1925年柯爾莫哥洛夫、Γ.A.謝利維奧爾斯托夫和A.普萊斯納的...
例如,對泛函分析中平方可積函式、平均收斂、運算元等的形成,對一般線性運算元理論的創立,以至於對整個泛函分析的形成都起著重要的推動作用。積分方程論中許多思想和方法...
如果一個函式在區間 [x0, x0+P]上是平方可積的,那么此傅立葉級數在幾乎所有點都收斂於該函式。傅立葉級數的收斂性取決於函式有限數量的極大值和極小值,這...
例如,對泛函分析中平方可積函式、平均收斂、運算元等的形成,對一般線性運算元理論的創立,以至於對整個泛函分析的形成都起著重要的推動作用。積分方程論中許多思想和方法...
設對稱核 k(x,y) 是G×G上的平方可積函式, K是以k(x,y)為核的線性積分運算元。若K僅有有限多個負特徵值,則稱k(x,y)必是擬正定核。...
與量子力學對應的希爾伯特空間是平方可積函式的空間。希耳伯空間在環境科學中 在環境綜合評價中,是以每種污染物相互獨立,互不相關的假設為前提的。這在數學上就成為...
作為希爾伯特空間的例子,除了歐幾里得空間和l空間以外,還有勒貝格平方可積函式空間 L^2[α,b](其中內積規定為(f,g)=f(t)g(t)(實數域)或f(t)乘以g(t)的...
3.海森堡群以及西哥爾區域上的可允許小波理論。導致平方可積函式空間的完全正交分解,具有基本的重要性。應有於中間亨格爾運算元研究,出色地解決了拉赫伯格的公開問題。...
線性積分運算元全連續性(complete continu-ity of linear integral operator)全連續性是線性積分運算元特有的基本性質.設k<x,婦是GXG上的平方可積函式,則以k(二,y)...
令X為一個在歐幾里得空間勒貝格可測集上的平方可積函式的希爾伯特空間,也就是說 是勒貝格可測集 。泛函 由 給出,其中 F 是一個定義在實數上的可微實值函式且...
拉普拉斯 - 貝爾特拉米運算元在流形上的本徵函式用作嵌入維數,因為在溫和條件下,該運算元具有可計數的譜,該譜是流形上的平方可積函式的基礎(與單位圓流形上的傅里...
即運算在此結構系統中暢行無阻.如在實變函式論中,勒貝格可積函式與平方可積函式概念的引人,就使1.,與1.Z均成為完備空間.這種抽象思維的法則可稱為:“新元...
