基本介紹
- 中文名:完備系
- 外文名:complete system
- 概述:具有某種完備性質的函式系
- 舉例:基本三角函式系
- 套用領域:泛函分析、數學物理方程等
- 學科:數學
定義

舉例


重要定理
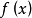






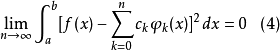

判斷準則
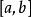
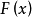


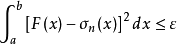



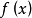






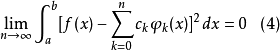

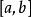
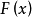


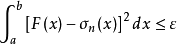
完備系(complete system)是具有某種完備性質的函式系。函式係為完備系的充分必要條件是:任意一個平方可積函式的傅立葉級數均值收斂於它本身。例如:定義在[-π,π...
完備,拼音wán bèi,注音ㄨㄢˊㄅㄟˋ英文complete leave nothing to be desired,含義:具備,不缺任何必要的東西的;完備的工具。...
弱F是H中的完全正交系,如果對每個x∈H,F使帕塞瓦爾等式成立,就稱F是完備正交系。...... 的完全正交系,如果對每個x∈H,F使帕塞瓦爾等式成立,就稱F是完備正交...
完備性是指在數學及其相關領域中,當一個對象具有完備性,即它不需要添加任何其他元素,這個對象也可稱為完備的或完全的。完備性也稱完全性,可以從多個不同的角度來...
在可計算性理論里,如果一系列運算元據的規則(如指令集、程式語言、細胞自動機)可以用來模擬單帶圖靈機,那么它是圖靈完備的。這個詞源於引入圖靈機概念的數學家艾倫...
《完備的辯證集合》是2018年由張信仿編著,四季出版社出版的圖書。作者通過數學假設和邏輯推理的方法,證明了唯物辯證法是正確的。並且還證明了至多只有兩個無窮基數...
《七步打造完備的培訓管理體系》是由作者苗海榮編寫,哈爾濱出版社出版的書籍。...... 《七步打造完備的培訓管理體系》是由作者苗海榮編寫,哈爾濱出版社出版的書籍。...
在可計算性理論里,如果一系列運算元據的規則(如指令集、程式語言、細胞自動機)可以用來模擬單帶圖靈機,那么它是圖靈完備的。這個詞源於引入圖靈機概念的數學家艾倫...
1. 七步打造完備的招聘管理體系 .豆瓣讀書[引用日期2013-02-28] 詞條標籤: 出版物 , 書籍 圖集 七步打造完備的招聘管理體系圖冊 V百科往期回顧 詞條統計 瀏覽...
設E是向量格,如果任何有上界的子集都必有上確界,則稱E是序完備的。...... 設E是向量格,如果任何有上界的子集都必有上確界,則稱E是序完備的。...
行完備拉丁方(row complete Latin square)是一類特殊的拉丁方,若n元集X的任意相異元的有序偶在X上的某個n階拉丁方的行中作為相鄰元素的有序偶至少出現一次,...
如果任何有上界的可數子集都必有上確界,則稱E是σ完備的。σ完備的向量格必是阿基米德向量格。...
grey system華中科技大學控制科學與工程系教授,博士生導師鄧聚龍於1982年提出的。它是用來解決信息不完備系統的數學方法,它把控制論的觀點和方法延伸到複雜的大系統中...
正交系是互相正交的函式系的簡稱,用於微分方程、積分方程、計算方法等數學領域。...... 是H中的標準正交系,則 是完備的,若且唯若 是完全的。在一般的希爾伯特空...
