基本介紹
釋義
























特例





性質
對偶空間















嵌入






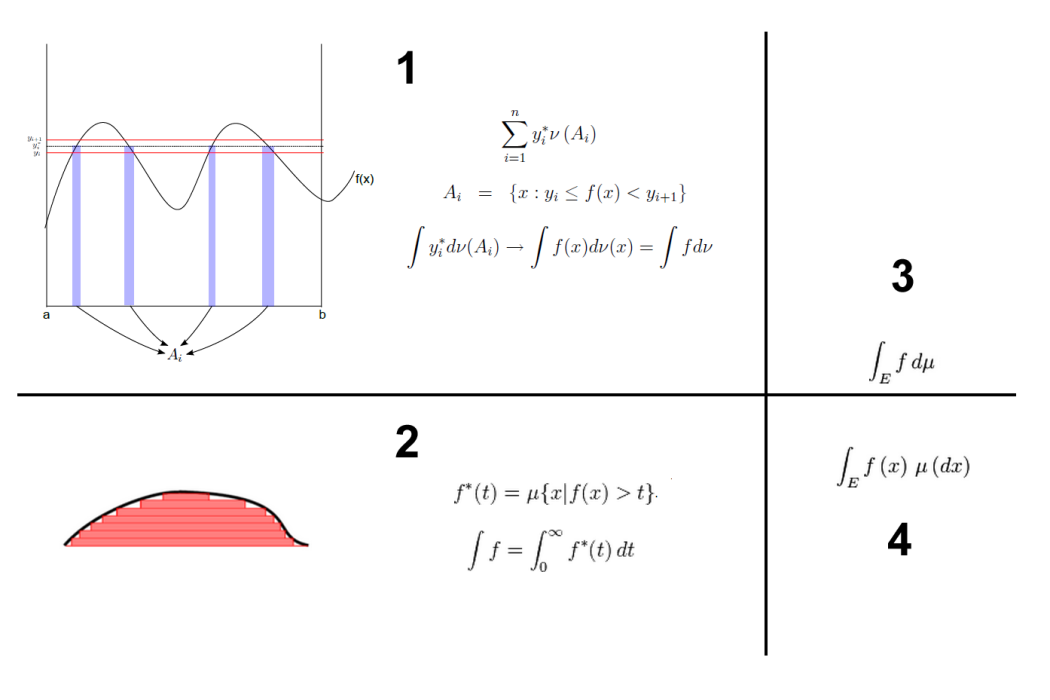


















































在數學中,Lp空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名,儘管依據Bourbaki (1987)它們是Riesz (1910)首先介入。在泛函分析...
例如,當𝓕是Rⁿ中的波萊爾集類𝓑時,(Rⁿ,𝓑)稱為波萊爾可測空間。當𝓕是Rⁿ中的勒貝格可測集類𝓛時,(Rⁿ,𝓛)稱為勒貝格可測空間。辨析:可測空間中的可測集和測度無關,測度空間中的可測集和測度有關。
在數學分析中,勒貝格定理,或稱黎曼-勒貝格定理是一個傅立葉分析方面的結果。這個定理有兩種形式,分別是關於周期函式(傅立葉理論中關於傅立葉級數的方面)和關於在一般實數域R上定義的函式(傅立葉變換的方面)。在任一種形式下,...
勒貝格數(Lebesgue number)是緊度量空間中與覆蓋有關的數。若X是緊度量空間,B是X的任意開覆蓋,則存在正數λ使得{B(x)|x∈X}是B的加細,其中B(x)為度量空間X中以x為中心λ為半徑的開球。正數λ稱為覆蓋B的勒貝格數。上述結論...
測度空間是定義了測度的可測空間。設(Ω,𝓕)是可測空間,μ是𝓕上的測度,(Ω,𝓕,μ)稱為測度空間。定義 勒貝格-斯蒂爾傑斯測度空間是定義了勒貝格-斯蒂爾傑斯測度的測度空間。勒貝格-斯蒂爾傑斯測度 勒貝格-斯蒂爾傑斯測度簡稱(L-...
空間是由p次可積函式組成的空間;對應的ℓp空間是由p次可和序列組成的空間。它們有時叫做勒貝格空間,以昂利·勒貝格命名(Dunford & Schwartz 1958,III.3),儘管依據Bourbaki (1987)它們是Riesz (1910)首先介入。在泛函分析和拓撲...
勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;勒貝格可測集A的體積或者說測度記作λ(A)。一個值為∞的勒貝格測度是...
的一個同構空間。特別地,當 的時候,可以將其簡單記為 。常見空間定義 歐幾里得空間 及其上的內積 構成了一個希爾伯特空間,其中短橫線表示一個複數的復共軛。勒貝格空間 勒貝格空間( 這裡指 空間 )是指定義在測度空間上的函...
勒貝格分解定理(Lebesgue decomposition theorem)是關於σ有限廣義測度分解為絕對連續部分和奇異部分之和的重要定理,是有界變差函式的勒貝格分解定理的推廣。設(Ω,F,μ)是σ有限測度空間,若γ是(Ω,F)上的σ有限測度,則γ可分解為...
縮小 F為小一點的σ域 F', 使得 F' 包括所有的區間, 而且其中的元素都有測度 L, 而且 L是區間長度概念的自然推廣, 就得到所謂勒貝格測度空間(R,F',L), F' 中的元素叫勒貝格可測集, 而相應的測度 L叫勒貝格測度。所以...
勒貝格內測度是勒貝格(Lebesgue,H.L.)提出他的測度定義時所用的一個輔助性概念,簡稱(L)內測度。簡介 勒貝格內測度是勒貝格(Lebesgue,H.L.)提出他的測度定義時所用的一個輔助性概念,簡稱(L)內測度。m*(E)=inf{G|G包含E且G為...
Lp空間 在數學中, L空間是由p次可積函式組成的空間;對應的L空間是由p次可和序列組成的空間。在泛函分析和拓撲向量空間中,他們構成了Banach空間一類重要的例子。L空間都是巴拿赫空間,但只有當p=2的時候,L空間是希爾伯特空間。也就...
為上所有實數值緊支撐連續函式所構成的空間。定義 的範數為 這樣一來 是一個賦范向量空間(特別地,它是一個度量空間)。所有的度量空間都有豪斯多夫完備性,因此令 為其完備空間。這個空間與勒貝格可積分函式余積分為零的子空間...
簡稱可測集。例如,當F是R中的博雷爾集類B時,(R,B)稱為博雷爾可測空間。當F是R中的勒貝格可測集類L時,(R,L)稱為勒貝格可測空間。可測空間是測度的定義域,在一個可測空間上可以定義不止一種測度。
簡稱可測集。例如,當F是R中的博雷爾集類B時,(R,B)稱為博雷爾可測空間。當F是R中的勒貝格可測集類L時,(R,L)稱為勒貝格可測空間。可測空間是測度的定義域,在一個可測空間上可以定義不止一種測度。
設F是基本空間Ω上的σ代數,稱(Ω,F)為可測空間,而稱F中的元素A是(Ω,F)中的可測集,也稱為Ω中的F可測集,簡稱可測集。例如,當F是R中的博雷爾集類B時,(R,B)稱為博雷爾可測空間。當F是R中的勒貝格可測集類L時...
若𝓕是X的σ代數,則稱(X,𝓕)為可測空間,𝓕中的元稱為X的可測集。勒貝格可測集 設 ,若對任意的點集 ,有 ,則稱E為勒貝格可測集,簡稱可測集。注意事項如下:(1)可測集的全體記為M,對於可測集E,稱其外...
完備測度(complete measure)亦稱完全測度,是使得零集的任何子集都可測的那種測度。設(Ω,F,μ)是測度空間,如果(Ω,F,μ)中μ零集的子集都是可測集,則稱μ是完備測度,並稱(Ω,F,μ)是完備測度空間。勒貝格測度空間和勒貝格-...
測度問題是測度論中的著名問題,是勒貝格(Lebesgue,H.L.)於1904年提出的。簡介 測度問題是測度論中的著名問題。對於直線而論,人們總希望直線上某個測度,關於它可測的集合越多越好。可測集多,意味著可測函式多,從而可積函式也多...
典型條件測度族(canonical system of condi-tional measures)測度論中一個十分重要的概念.它的存在性是勒貝格空間可測分割的一個重要性質,利用它人們可以用一般的可測分割來討論嫡 典型條件測度族,測度論中一個十分重要的概念.它的存在...
設F是基本空間Ω上的σ代數,稱(Ω,F)為可測空間,而稱F中的元素A是(Ω,F)中的可測集,也稱為Ω中的F可測集,簡稱可測集。例如,當F是R中的波萊爾集類B時,(R,B)稱為波萊爾可測空間。當F是R中的勒貝格可測集類L時...
在一般拓撲空間中可類似地引入博雷爾集。測度 測度,是數學術語,釋義是構造一個集函式,它能賦予實數集簇М中的每一個集合E一個非負擴充實數m(E)。我們將此集函式稱為E的測度。測度有計數測度、勒貝格測度、哈爾測度、機率測度等。...
勒貝格測度 勒貝格測度:實數集R上的勒貝格測度不是有限測度,因為整個實數軸的“長度”,也就是全集R的測度是無窮大。但是,勒貝格測度是σ-有限測度,因為R可以表示為所有形如[-n,n]的區間的並集,而每個區間的測度都是有限的(等於...
勒貝格測度 勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛套用於實分析,特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測;勒貝格可測集A 的體積或者說測度記作 λ(A) 。一個值為 ...
設A是測度空間(Ω,𝓕,μ)中的可測集。如果μ(A)=0,則稱A為μ零集。性質 空集是任何測度的零集;有限集和可數集是勒貝格測度的零集。測度論 測度論是研究一般集合上的測度和積分的理論。它是勒貝格測度和勒貝格積分理論的進一步...
可測分割(measurable partition)勒貝格空間條件測度理論的基礎.設(X,.},川為機率空間,X的一族互不相交且並等於X的非空子集就稱為X的一個分割.設g為X的一個分割,若AC.}可以表示成夸中若干個元素的並,則稱A為夸集.設}A}IyE....
