基本介紹
- 中文名:伴隨表示
- 外文名:adjoint representation
- 所屬學科:李群
- 定義:代數群在它的李代數上的典範表示
- 類別:代數群的一種表示
- 類型:李群名詞
定義
等價定義
表示



伴隨表示






伴隨表示的性質


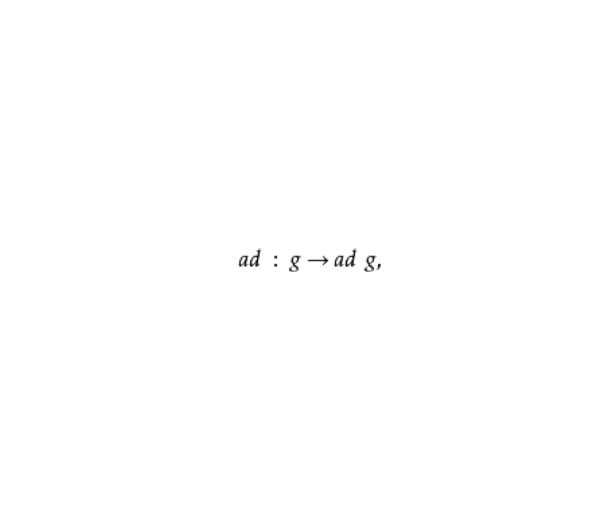











伴隨表示(adjoint representation)是代數群的一種表示,指代數群在它的李代數上的一個典範表示。設G是代數群,g是它的李代數,G在g上的伴隨表示定義為Ad:G→Aut(g)⊂GL(g):對g∈G與X∈g...
伴隨表示(adjoint representation)是代數群的一種表示,指代數群在它的李代數上的一個典範表示。設G是代數群,g是它的李代數,G在g上的伴隨表示定義為Ad:G→Aut(g)⊂GL(g):對g∈G與X∈g,Adg(X)=ρgXρg-1。例如,當G=GL...
一、with複合結構做伴隨狀語:由“with+賓語+賓語補足語”構成的複合結構,在句中可作狀語,表示伴隨。這一結構中的賓語補足語可由現在分詞、過去分詞、形容詞、副詞或介詞短語等來充當。例如:1.With production up by 60%, the ...
撓伴隨表示(twisted adjoint representation)克利福德代數乘法群的一種表示.設E是特徵為零的域K上的n維向量空間,(,)是E上的非退化雙線性對稱函式,CE是C:中可逆元的乘法群,由ad(a)u=WECa)ua-‘定義的ad稱為CE的撓伴隨表示,...
經典伴隨變換(classical adjoint transformation)是向量空間中的一種線性變換。線上性代數中,一個方形矩陣的伴隨矩陣是一個類似於逆矩陣的概念。如果矩陣可逆,那么它的逆矩陣和它的伴隨矩陣之間只差一個係數。然而,伴隨矩陣對不可逆的矩陣...
隨著量子群和量子Yang-Baxter方程解的聯繫建立,量子化包絡代數和量子Schur代數理論取得了極大的發展,關於它們的結構、表示和實現問題成為目前國際代數學家關注的重要問題之一。本課題首先利用伴隨表示研究有限維單李超代數的量子化包絡代數的...
利用里斯表示定理,我們可以證明存在惟一的連續線性運算元 A*:H→H具有如下性質:,對所有 。這個運算元A* 是A的伴隨。這可以視為一個方塊矩陣的轉置共軛或伴隨矩陣推廣,在標準(復)內積下具有相似的性質。性質 可得性質:A** =A 如A...
伴隨模式是時空軌跡模式中的一種,在交通管理,資源分配等領域有著重要的套用。時空軌跡的定義 時空軌跡是移動對象的位置和時間的記錄序列。簡單來說,時空軌跡是時間到空間的映射,假設由一個以時間為自變數的連續函式o表示,當給定某一...
的一個表示,其表示空間就是 本身,稱為 的伴隨表示。則 為阿貝爾李代數,若且唯若對 中所有X,ad X=0。伴隨表示的核稱為 的中心。設(ρ,V)是g的一個有限維表示。定義一個對稱雙線性型 k:g×g→F;對於X、Y ∈g, 定義...
表示的直積化直和,生成伴隨表示8,就可以給出對輕夸克組成的介子的8重態分類,具體見圖3:發展歷史 1961年蓋爾曼在奇異數守恆定律的基礎上,又提出了SU(3)對稱性。對強相互作用的粒子進一步作出分類。效仿佛教的“八正道”(即“...
伴隨表示 在數學中,一個李群G的伴隨表示(adjoint representation)或伴隨作用(adjoint action)是G在它自身的李代數上的自然表示。這個表示是群G在自身上的共軛作用的線性化形式。默里·蓋爾曼 默里·蓋爾曼(英語:Murray Gell-Mann,...
但為了整體描述方便起見,取聯絡的坐標表示,這裡u-1du是群G的左不變形式,αd是伴隨表示。當M=∪Up,把粘合起來便得主叢P,這時若x∈Up∩Uq,把(x,up)和(x,uq)視為同一元素,但up和uq之間要由轉換函式up=gpquq所聯繫(這裡...
表示運算元 的伴隨運算元。事實上,對於一個適當的希爾伯特空間 ,每個 C*-代數 都 *-同構於 的閉范伴隨閉子代數(norm-closed adjoint closed subalgebra);這就是蓋爾范徳-奈馬克定理(Gelfand–Naimark theorem)的內容。緊運算元 設 是...
10 伴隨表示 11 覆蓋群 12 Riemann流形 習題 第四章 半單純李代數的結構 1 可解李代數和可解李群 2 冪零李代數和冪零李群 3 半單純李代數和緊緻李群的分 4 緊緻連通李群的極大子環群 5 半單純李代數的根系 6 半單純李代數的...
③作方式狀語,表示伴隨:He stayed at home,cleaning and washing. 他呆在家裡,又擦又洗。④作條件狀語:(If) Playing all day,you will waste your valuable time.要是整天玩,你就會浪費寶貴的時間。⑤作結果狀語:He dropped ...
6.9 lorentz群及其表示 6.10 經典lie群的張量表示 習題6 第7章 lie代數 7.1 lie代數 7.2 伴隨表示 7.3 killing形式 7.4 單根與dynkin圖 7.5 權與lie代數的表示 7.6 casimir算符 習題 習題答案與提示 附錄 附錄a 線性代數...
我們證明了當物質場也在規範群的伴隨表示中的時候,pioncare超對稱能夠從N=(1,0)提升到最大超對稱(2,0)。此外我們還構建和研究了理論的超流(supercurrent). 我們利用維數約化技術,從這個新構建的6維(1,0)理論導出了5維中超對稱...
我喜歡把窗戶開著睡覺。(伴隨情況)2.With the weather so close and stuffy, ten to one it'll rain presently.大氣這樣悶,十之八九要下雨(原因狀語)二、with或without+名詞/代詞+副詞 例句:1.She left the room with all...
3.9.4 李代數的表示 3.10 李運算與李括弧及其等價原理 3.10.1 標準4×4 矩陣表示的李括弧 3.10.2 交換子與jacobi恆等式 3.10.3 6×6 伴隨表示的李括弧及其等價定理 參考文獻 第四章位移運算元與指數映射 4.1 坐標變換 4....
第三章 伴隨變換的幾何 1伴隨變換與伴隨表示 2極大子環群 3權系、根系和Cartan分解 4伴隨變換的軌幾何 5Weyl公式和復不可約表示的分類 第四章 緊緻連通李群的結構與分類 1緊緻李代數 2根系、Cartan分解與緊緻李代數的結構 3分類...
附錄26 SU(N)群自身表示生成元的反對易關係 附錄27 實贗正交矩陣的行列式 附錄28 辛群獨立實參數的數目 附錄29 單純李代數的重要性質 附錄30 克萊布施一戈登係數的對稱性質 附錄31 SU(3)群兩伴隨表示直乘的克萊布施一戈登係數 ...
附錄26 SU(N)群自身表示生成元的反對易關係 附錄27 實贗正交矩陣的行列式 附錄28 辛群獨立實參數的數目 附錄29 單純李代數的重要性質 附錄30 克萊布施一戈登係數的對稱性質 附錄31 SU(3)群兩伴隨表示直乘的克萊布施-戈登係數 附錄...
to,英文單詞,介詞、副詞、名詞,作介詞時意為“朝;位於……;到某處;到某狀態;差;給;對於;比;連著;對著;等於;向……表示敬意;伴隨;為了給……;適合;按……的看法;(結算賬目時)記入”,作副詞時意為“(門等)...
書店通常在下午7:30關門。(被動語態,表示動作)作狀語 作時間、條件、原因、讓步狀語時要位於句首,且與後面用逗號隔開。能轉換為一個相應的狀語從句。作結果、方式、伴隨狀語時要位於句尾,且與前面用逗號隔開,有時也可以不用。...
