mKdV方程是一個非線性偏微分方程。
基本介紹
- 中文名：Mkdv方程
- 外文名：mKdV equation
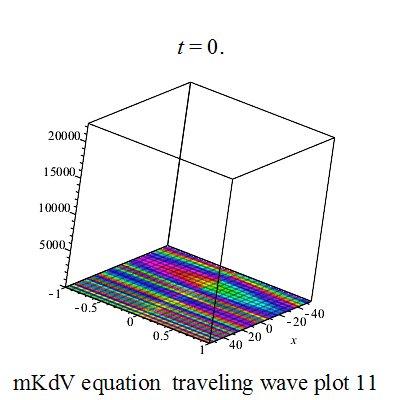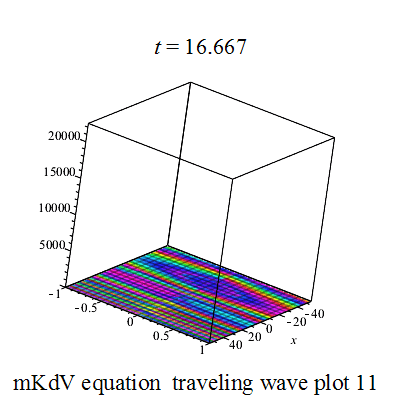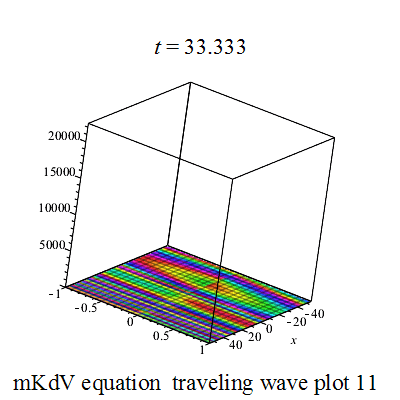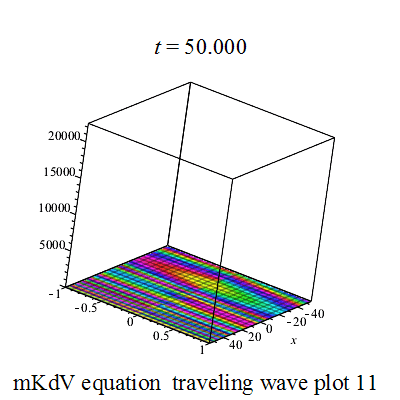
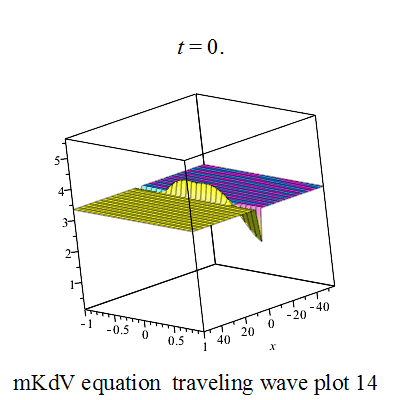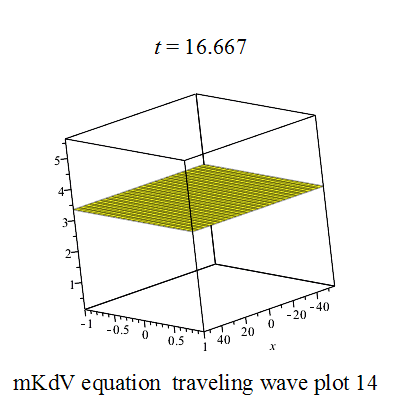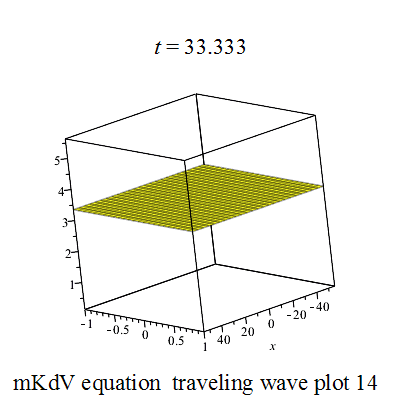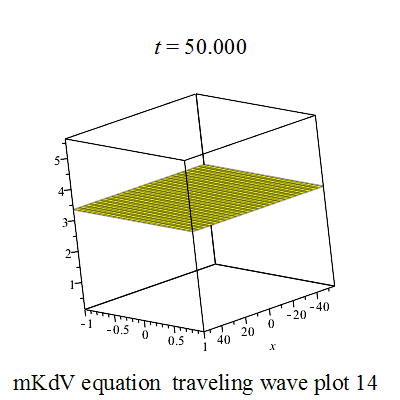
非線性偏方法方程,行波解,
非線性偏方法方程
行波圖
行波圖
行波圖
行波解
mKdV方程
相關詞條
- 廣義KdV方程和D-S方程適定性問題
《廣義KdV方程和D-S方程適定性問題》是依託江蘇大學，由沈彩霞擔任項目負責人的數學天元基金項目。項目摘要 本課題主要研究四個方面的內容:1. 討論mKdV方程的初邊值問題. 得到線性估計和三線性估計， 然後證明了四分之一平面上的mKdV...
- 孤波方程滿足多個守恆律的數值方法
最後我們將這種滿足兩個守恆律的思想套用到更一般的孤波方程，即mKdV方程，對其設計滿足兩個守恆律的方法，採用分裂運算元法，將其分成非線性守恆方程部分和三階線性散射方程部分，將滿足兩個守恆律的技巧套用到守恆方程部分，對三階散射方程...
- 非線性偏微分方程列表
簡要介紹 主條目：Tanh 函式展開法 Tanh 函式展開法是求解非線性偏微分方程行波解的重要方法。設一個非線性偏微分方程可以用下列表述：作變數代換：-> 得到：1992年數學家 Malfliet 首先套用 tanh 展開法 對稱分析 Lax 可積系統 ...
- 變分方法和幾何奇異攝動理論及其在微分方程中的套用
得到了解的存在性、唯一性，並給出了攝動解的一致有效的漸近估計；綜合運用幾何奇異攝動理論、線性鏈技巧和Fredholm定理等，研究不含時滯、帶有局部時滯核心和帶有非局部時滯核心的三種情況下的廣義KdV-mKdV 方程，得到了該方程在三種情況...
- 非線性離散可積方程與離散Painlevé方程族的連續極限理論
通過構造非均勻譜Volterra方程族，非均勻譜離散mKdV方程族，非均勻譜離散Boussinesq 方程族的連續極限理論，建立離散Painlevé (I, II, III)方程族與Painlevé (I, II, III)方程族之間的一一對應關係，進一步研究離散Painlevé方程及其族的...
- 非線性薛丁格型方程的怪波解
利用達布變換， 提出了高階怪波的構造方法，並提出行程機制：n階怪波來來自n個互相子的雙重退化，從而證明了n階怪波峰個數和圓圈分解規律這兩個猜想； 引入了怪波局域性刻畫方法：對復mKdV方程的怪波解，通過等高線定義其長，寬和面積...
- 微分方程的李群方法
2.1 常微分方程在正則坐標下的精確解.44 2.1.1 一階常微分方程情形 .44 2.1.2 二階常微分方程情形 .46 2.2 幾類偏微分方程的不變解與精確解.52 2.2.1 (1+1) 維熱方程情形 52 2.2.2 組合 KdV-mKdV 方程情形 55...
- 非線性偏微分方程
非線性偏微分方程是各階微分項有次數高於一的微分方程即為非線性偏微分方程，是現代數學的一個重要分支，無論在理論中還是在實際套用中，非線性偏微分方程均被用來描述力學、控制過程、生態與經濟系統、化工循環系統及流行病學等領域的...
- 離散可積系統的Darboux變換,精確解及其解的動力學性質
我們研究了一個半離散mKdV方程系統，一個Volterra方程系統，一個高階半離散mKdV方程的連續極限理論，證明了在連續極限下它們的可積性（包括Lax 對，Darboux變換，孤子解，無窮守恆律 ）導致到對應的連續可積系統的可積性。這些主要研究...
- 孤子理論和微擾方法
17薩哈諾夫－沙巴特反散射方程 18散射數據隨時間的演化 191－孤子解 20無反射情況 21N－孤子解的顯式 222－孤子解 23N－孤子解的漸近行為 24孤子解的驗證 25NLS方程的無窮多個守恆量 第3章 MKdV方程、SG方程和L－L方程 26MKdV...
- 可積系統在數值算法中的套用
三，孤子方程的可積離散化及數值套用方面：我們給出了mKdV方程的可積半離散化，然後將時間方向的可積離散與空間方向的擬譜法離散結合在一起，成功構造出一種快速有效求解mKdV方程的數值格式。我們的研究豐富了可積系統在數值算法中的套用...
- 齊性空間中的不變曲線流和對偶可積系統
我們的主要結果如下：我們建立了Symplectic-Grassman空間G(2,4)上正則曲線的Serret-Frenet公式和平行標架公式，證明了矩陣mKdV方程可以幾何實現為G(2,4)上的不變曲線流，並得到了矩陣mKdV方程的幾何雙哈密頓結構和遞推運算元。我們證明了...
- 非線性數學物理方法
第二章 非線性數學物理方程的導出 2.1 VCKdV型方程的導出 2.2 VCMKdV型方程的導出 2.3 VCNLS型方程的導出 2.4 耦合KdV方程的導出 第三章 非線性方程的行波法 3.1 線性波動方程的行波法 3.2 非線性系統的行波約化 3...
- 力學分析中的對稱性和守恆律
11.1 KdV方程的變分對稱性 292 11.2 KdV方程的高階對稱性 294 11.2.1 伴隨方程與Lagrange函式 294 11.2.2 守恆律 295 11.3 擾動KdV方程的高階近似對稱性 301 11.4 mKdV方程的Ibragimov守恆律 305 11.4.1 ...
- 物理中的幾何流與幾何孤立子
在此基礎上，本項目研究探索了物理中幾類經典方程在流形上統一的幾何描述，我們提出了薛丁格-Airy幾何流的定義來統一復向量值mKdV方程，薛丁格方程，導數非線性薛丁格方程，Airy方程，渦絲運動方程等物理方程；同時我們還在完備黎曼流形上定義...
- 可積系統、正交多項式和隨機矩陣——Riemann-Hilbert方法
主題部分取材於Deift、McLaughlin、Biondini、Jenkins等一些學者近年來*新前沿成果.內容主要包括Riemann-Hilbert方法與方程的零邊界和非零邊界求解；Deift-Zhou非線性速降法與mKdV方程的長時間漸近性；速降法與方程在孤子區域的長時間漸近性；...
- 關於不可壓縮流體的粘性消失極限問題
2+1）維MKdV方程及反對稱NNV方程同構的幾類新的方程組,並對其中一個得到的方程建立了群不變解;研究了一類三階KdV型非線性發展方程的Galilei對稱並對其中一個得到的Galilei不變方程作了完全群不變解的分類.推廣了非線性發展方程切對稱...
- 阮傳同
阮傳同，1979年10月出生，河南省淮陽人，中共黨員， 碩士，講師.研究領域 機率統計,孤立子與可積系統.主講課程 機率統計、機率論與數理統計.學術成果 發表論文 1. 耦合離散mKdV方程的達布變換及其精確解 周口師範學院學報 2010.10 2....
- 離散與連續的有限維可積系統及其套用
利用此種工具，有效地算出一系列全離散可積方程的有限虧格解，包括著名的ABS單子中譜參數空間虧格為零情形的全部方程，即H1，H3(0)和Q1(0)，全離散的KdV，SG和MKdV方程，以及ABS單子外的幾個方程，包括AKNS族導出的三個新的全離散...
- 可積系統的代數與幾何結構
揭示耦合mKdV方程與斜正交多項式、收斂加速算法和 Laurent性質間的關係。定義了超對稱微分多項式的符號表示，並用其實現了超對稱微分多項式的相關運算。進而給出一類超對稱發展型方程的完整可積分類。我們獲得超對稱sine-Gordon、超對稱mKdV、...
- 非線性物理學中若干機械化算法的研究
設計了一個構造KdV-型方程雙線性形式、雙線性Backlund變換、Lax對和無窮守恆律的機械化算法。開發了實現該算法的軟體包PDEBellII。 程式包也適用於mKdV-型方程雙線性形式的自動推演。將Bell多項式方法套用到一些(1+1)維、(2+1)維和變...
- 孤波
孤波解是一類特殊的非線性偏微分方程的行波解。KdV方程、mKdV方程、非線性薛丁格方程、sine-Gordon方程和高次Boer-Kraup 系統都有孤波解。分類 孤波有如下幾種類型：鐘型孤波、反鐘形孤波、扭型孤波、反扭型孤波，呼吸子等。套用...
- 非線性系統可積性的若干機械化算法及套用研究
（4）發展和提出了直接分離變數法，研究了（2+1）維mKdV方程、（3+1）維BKP方程、（3+1）破碎孤子方程等高維非線性方程，得到了其豐富的局域激發模式；（5）改進了基方程展開法，研究了具有強非線性項的幾個非線性演化方程的精確...
- 定態微擾論
對於大量的實際物理問題，Schrodinger方程能有精確解的情況很少。通常體系的 Hamilton 量是比較複雜的，往往不能精確求解。因此，在處理複雜的實際問題時，量子力學求問題近似解的方法（簡稱近似方法）就顯得特別重要。微擾論是各種近似方法中...
