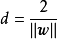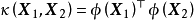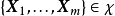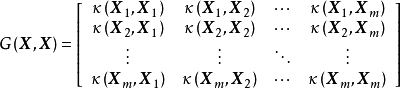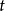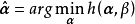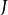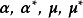歷史 SVM是由模式識別中廣義肖像算法(generalized portrait algorithm)發展而來的分類器,其早期工作來自前蘇聯學者Vladimir N. Vapnik和Alexander Y. Lerner在1963年發表的研究。1964年,Vapnik和Alexey Y. Chervonenkis對廣義肖像算法進行了進一步討論並建立了硬邊距的線性SVM。此後在二十世紀70-80年代,隨著模式識別中最大邊距決策邊界的理論研究、基於
鬆弛變數 (slack variable)的規劃問題求解技術的出現,和
VC維 (Vapnik-Chervonenkis dimension, VC dimension)的提出,SVM被逐步理論化並成為
統計學習理論 的一部分。1992年,Bernhard E. Boser、Isabelle M. Guyon和Vapnik通過
核方法 得到了非線性SVM。1995年,Corinna Cortes和Vapnik提出了軟邊距的非線性SVM並將其套用於手寫字元識別問題,這份研究在發表後得到了關注和引用,為SVM在各領域的套用提供了參考。
理論 線性分類 線性可分性(linear separability )
線性可分:決策邊界(實),間隔邊界(虛),支持向量(紅點) 在分類問題中給定輸入數據和學習目標:
,其中輸入數據的每個樣本都包含多個特徵並由此構成特徵空間(feature space):
,而學習目標為二元變數
表示負類(negative class)和正類(positive class)。
若輸入數據所在的特徵空間存在作為
決策邊界 (decision boundary)的
超平面 將學習目標按正類和負類分開,並使任意樣本的
點到平面距離 大於等於1:
則稱該分類問題具有線性可分性,參數
分別為超平面的法向量和截距。
滿足該條件的決策邊界實際上構造了2個平行的超平面作為間隔邊界以判別樣本的分類:
所有在上間隔邊界上方的樣本屬於正類,在下間隔邊界下方的樣本屬於負類。兩個間隔邊界的距離
被定義為邊距(margin),位於間隔邊界上的正類和負類樣本為
支持向量 (support vector)。
損失函式(loss function) 0-1損失函式和其代理損失,紅實線為0-1損失,黑實線為鉸鏈損失。 在一個分類問題不具有線性可分性時,使用超平面作為決策邊界會帶來分類損失,即部分支持向量不再位於間隔邊界上,而是進入了間隔邊界內部,或落入決策邊界的錯誤一側。
損失函式 可以對分類損失進行量化,其按數學意義可以得到的形式是0-1損失函式:
0-1損失函式不是
連續函式 ,不利於最佳化問題的求解,因此通常的選擇是構造代理損失(surrogate loss)。可用的選擇包括鉸鏈損失函式(hinge loss)、logistic損失函式(logistic loss)、和指數損失函式(exponential loss),其中SVM使用的是鉸鏈損失函式:
對替代損失的相合性研究表明,當代理損失是連續
凸函式 ,並在任意取值下是0-1損失函式的
上界 ,則求解代理損失最小化所得結果也是0-1損失最小化的解。鉸鏈損失函式滿足上述條件。
經驗風險(empirical risk)與結構風險(structural risk)
按統計學習理論,分類器在經過學習並套用於新數據時會產生風險,風險的類型可分為經驗風險和結構風險:
式中
表示分類器,經驗風險由損失函式定義,描述了分類器所給出的分類結果的準確程度;結構風險由分類器參數矩陣的範數定義,描述了分類器自身的複雜程度以及穩定程度,複雜的分類器容易產生過擬合,因此是不穩定的。若一個分類器通過最小化經驗風險和結構風險的
線性組合 以確定其模型參數:
則對該分類器的求解是一個正則化問題,常數
是正則化係數。當
時,該式被稱為L
2 正則化或Tikhonov正則化(Tikhonov regularization)。SVM的結構風險按
表示,線上性可分問題下,硬邊界SVM的經驗風險可以歸0,因此其是一個完全最小化結構風險的分類器;線上性不可分問題中,軟邊界SVM的經驗風險不可歸0,因此其是一個L
2 正則化分類器,最小化結構風險和經驗風險的線性組合。
核方法 一些線性不可分的問題可能是非線性可分的,即特徵空間存在
超曲面 (hypersurface)將正類和負類分開。使用非線性函式可以將非線性可分問題從原始的特徵空間映射至更高維的
希爾伯特空間 (Hilbert space)
,從而轉化為線性可分問題,此時作為決策邊界的超平面表示如下:
式中
為映射函式。由於映射函式具有複雜的形式,難以計算其
內積 ,因此可使用核方法(kernel method),即定義映射函式的內積為
核函式 (kernel function):
以迴避內積的顯式計算。
Mercer定理 (Mercer's theorem)
核函式的選擇需要一定條件,函式
是核函式的充要條件是,對輸入空間的任意向量:
,其核矩陣(kernel matrix),即如下形式的
格拉姆矩陣 (Gram matrix):
是
半正定矩陣 。上述結論被稱為
Mercer定理 。定理的證明從略,結論性地,作為充分條件:特徵空間內兩個函式的內積是一個
二元函式 ,在其核矩陣為半正定矩陣時,該二元函式具有可再生性:
,因此其內積空間是一個
賦范向量空間 (normed vector space),可以完備化得到
希爾伯特空間 ,即再生核希爾伯特空間(Reproducing Kernel Hilbert Space, RKHS)。作為必要條件,對核函式構造核矩陣後易知:
。
常見的核函式
在構造核函式後,驗證其對輸入空間內的任意格拉姆矩陣為半正定矩陣是困難的,因此通常的選擇是使用現成的核函式。以下給出一些核函式的例子,其中未做說明的參數均是該核函式的
超參數 (hyper-parameter):
名稱 解析式 多項式核(polynomial kernel)
拉普拉斯核(Laplacian kernel)
Sigmoid核(Sigmoid kernel)
當多項式核的階為1時,其被稱為線性核,對應的非線性分類器退化為線性分類器。RBF核也被稱為高斯核(Gaussian kernel),其對應的映射函式將樣本空間映射至無限維空間。核函式的
線性組合 和
笛卡爾積 也是核函式,此外對特徵空間內的函式
,
也是核函式。
算法 標準算法 線性SVM(linear SVM)
1. 硬邊距(hard margin)
給定輸入數據和學習目標:
,硬邊界SVM是線上性可分問題中求解最大邊距超平面(maximum-margin hyperplane)的算法,
約束條件 是樣本點到決策邊界的距離大於等於1。硬邊界SVM可以轉化為一個等價的二次凸最佳化(quadratic convex optimization)問題進行求解:
由上式得到的決策邊界可以對任意樣本進行分類:
。注意到雖然超平面法向量
是唯一最佳化目標,但學習數據和超平面的截距通過約束條件影響了該最佳化問題的求解。硬邊距SVM是正則化係數取0時的軟邊距SVM,其對偶問題和求解參見軟邊距SVM,這裡不額外列出。
2. 軟邊距(soft margin)
線上性不可分問題中使用硬邊距SVM將產生分類誤差,因此可在最大化邊距的基礎上引入損失函式構造新的最佳化問題。SVM使用鉸鏈損失函式,沿用硬邊界SVM的最佳化問題形式,軟邊距SVM的最佳化問題有如下表示:
上式表明可知,軟邊距SVM是一個L
2 正則化分類器,式中
表示鉸鏈損失函式。使用
鬆弛變數 :
處理鉸鏈損失函式的分段取值後,上式可化為:
求解上述軟邊距SVM通常利用其最佳化問題的
對偶性 (duality),這裡給出推導:
定義軟邊距SVM的最佳化問題為原問題(primal problem),通過
拉格朗日乘子 (Lagrange multiplier):
可得到其拉格朗日函式:
令拉格朗日函式對最佳化目標
的偏導數為0,可得到一系列包含拉格朗日乘子的表達式:
將其帶入拉格朗日函式後可得原問題的對偶問題(dual problem):
對偶問題的約束條件中包含不等關係,因此其存在局部最優的條件是拉格朗日乘子滿足Karush-Kuhn-Tucker條件(Karush-Kuhn-Tucker condition, KKT):
由上述KKT條件可知,對任意樣本
,總有
或
,對前者,該樣本不會對決策邊界
產生影響,對後者,該樣本滿足
意味其處於間隔邊界上(
)、間隔內部(
)或被錯誤分類(
),即該樣本是支持向量。由此可見,軟邊距SVM決策邊界的確定僅與支持向量有關,使用鉸鏈損失函式使得SVM具有稀疏性。
非線性SVM(nonlinear SVM)
使用非線性函式將輸入數據映射至高維空間後套用線性SVM可得到非線性SVM。非線性SVM有如下最佳化問題:
注意到式中存在映射函式內積,因此可以使用核方法,即直接選取核函式:
。非線性SVM的對偶問題的KKT條件可同樣類比軟邊距線性SVM。
數值求解
SVM的求解可以使用二次凸最佳化問題的數值方法,例如
內點法 和
序列最小最佳化算法 ,在擁有充足學習樣本時也可使用隨機梯度下降。這裡對以上3種數值方法在SVM中的套用進行介紹。
1. 內點法(Interior Point Method, IPM)
以軟邊距SVM為例,IPM使用對數阻擋函式(logarithmic barrier function)將SVM的對偶問題由極大值問題轉化為極小值問題並將其最佳化目標和約束條件近似表示為如下形式:
式中
為對數阻擋函式,在本質上是使用連續函式對約束條件中的不等關係進行近似。對任意超參數
,使用
牛頓疊代法 (Newton-Raphson method)可求解
,該數值解也是原對偶問題的近似解:
。
IPM在計算
時需要對N階矩陣求逆,在使用牛頓疊代法時也需要計算Hessian矩陣的逆,是一個記憶體開銷大且複雜度為
的算法,僅適用於少量學習樣本的情形。一些研究通過低秩近似(low-rank approximation)和並行計算提出了更適用於大數據的IPM,並在SVM的實際學習中進行了套用和比較。
2. 序列最小最佳化(Sequential Minimal Optimization, SMO)
SMO是一種
坐標下降法 (coordinate descent),以疊代方式求解SVM的對偶問題,其設計是在每個疊代步選擇拉格朗日乘子中的兩個變數
並固定其它參數,將原最佳化問題化簡至1維子可行域(feasible subspace),此時約束條件有如下等價形式:
將上式右側帶入SVM的對偶問題並消去求和項中的
可以得到僅關於
的二次規劃問題,該最佳化問題有閉式解可以快速計算。在此基礎上,SMO有如下計算框架:
初始所有化拉格朗日乘子;
識別一個不滿足KKT條件的乘子,並求解其二次規劃問題;
反覆執行上述步驟直到所有乘子滿足KKT條件或參數的更新量小於設定值。
可以證明,在二次凸最佳化問題中,SMO的每步疊代都嚴格地最佳化了SVM的對偶問題,且疊代會在有限步後收斂於全局極大值。SMO算法的疊代速度與所選取乘子對KKT條件的偏離程度有關,因此SMO通常採用啟發式方法選取拉格朗日乘子。
3. 隨機梯度下降(Stochastic Gradient Descent, SGD)
SGD是機器學習問題中常見的最佳化算法,適用於樣本充足的學習問題。SGD每次疊代都隨機選擇學習樣本更新模型參數,以減少一次性處理所有樣本帶來的記憶體開銷,其更新規則如下:
式中梯度前的係數是學習速率(learning rate),
是
代價函式 (cost function)。由於SVM的最佳化目標是
凸函式 ,因此可以直接將其改寫為極小值問題並作為代價函式運行SGD。以非線性SVM為例,其SGD疊代規則如下:
由上式可知,在每次疊代時,SGD首先判定約束條件,若該樣本不滿足約束條件,則SGD按學習速率最小化結構風險;若該樣本滿足約束條件,為SVM的支持向量,則SGD根據正則化係數平衡經驗風險和結構風險,即SGD的疊代保持了SVM的稀疏性。
編程實現
這裡提供一個python 3環境下使用scikit-learn封裝模組的SVM編程實現:
# 導入模組import numpy as npimport matplotlib.pyplot as pltfrom sklearn import svm, datasets% matplotlib inline# 鳶尾花數據iris = datasets.load_iris()X = iris.data[:, :2] # 為便於繪圖僅選擇2個特徵y = iris.target# 測試樣本(繪製分類區域)xlist1 = np.linspace(X[:, 0].min(), X[:, 0].max(), 200)xlist2 = np.linspace(X[:, 1].min(), X[:, 1].max(), 200)XGrid1, XGrid2 = np.meshgrid(xlist1, xlist2)# 非線性SVM:RBF核,超參數為0.5,正則化係數為1,SMO疊代精度1e-5, 記憶體占用1000MBsvc = svm.SVC(kernel='rbf', C=1, gamma=0.5, tol=1e-5, cache_size=1000).fit(X, y)# 預測並繪製結果Z = svc.predict(np.vstack([XGrid1.ravel(), XGrid2.ravel()]).T)Z = Z.reshape(XGrid1.shape)plt.contourf(XGrid1, XGrid2, Z, cmap=plt.cm.hsv)plt.contour(XGrid1, XGrid2, Z, colors=('k',))plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', linewidth=1.5, cmap=plt.cm.hsv) 改進算法 偏斜數據的改進算法
軟邊距的線性和非線性SVM可以通過修該其正則化係數為偏斜數據賦權。具體地,若學習樣本中正例的數量遠大於負例,則可按樣本比例設定正則化係數:
式中的
表示正例和負例,即在正例多時,對正利使用小的正則化係數,使SVM傾向於通過正例降低結構風險,同時也對負例使用大的正則化係數,使SVM傾向於通過負例降低經驗風險。
機率SVM(Platt's probabilistic outputs)
機率SVM可以視為Logistic回歸和SVM的結合,SVM由決策邊界直接輸出樣本的分類,機率SVM則通過
Sigmoid函式 計算樣本屬於其類別的機率。具體地,在計算標準SVM得到學習樣本的決策邊界後,機率SVM通過縮放和平移參數
對決策邊界進行
線性變換 ,並使用
極大似然估計 (Maximum Liklihood Estimation, MLE)得到
的值,將樣本到線性變換後超平面的距離作為Sigmoid函式的輸入得到機率。在通過標準SVM求解決策邊界後,機率SVM的改進可表示如下:
式中第一行的最佳化問題實際上是縮放和平移參數的
Logistic回歸 ,需要使用梯度下降算法求解,這意味著機率SVM的運行效率低於標準SVM。在通過學習樣本得到縮放和平移參數的MLE後,將參數套用於測試樣本可計算SVM的輸出機率。
多分類SVM(multiple class SVM)
標準SVM是基於二元分類問題設計的算法,無法直接處理多分類問題。利用標準SVM的計算流程有序地構建多個決策邊界以實現樣本的多分類,通常的實現為“一對多(one-against-all)”和“一對一(one-against-one)”。一對多SVM對m個分類建立m個決策邊界,每個決策邊界判定一個分類對其餘所有分類的歸屬;一對一SVM是一種投票法(voting),其計算流程是對m個分類中的任意2個建立決策邊界,即共有
個決策邊界,樣本的類別按其對所有決策邊界的判別結果中得分最高的類別選取。一對多SVM通過對標準SVM的最佳化問題進行修改可以實現一次疊代計算所有決策邊界。
最小二乘SVM(Least Square SVM, LS-SVM)
LS-SVM是標準SVM的一種變體,兩者的差別是LS-SVM沒有使用鉸鏈損失函式,而是將其最佳化問題改寫為類似於嶺回歸(ridge regression)的形式,對軟邊距SVM,LS-SVM的最佳化問題如下:
類比標準SVM,可以通過拉格朗日乘子:
得到LS-SVM的對偶問題,該對偶問題是一個線性系統:
上述公式可以使用核方法得到非線性LS-SVM。LS-SVM的線性系統可以通過
共軛梯度法 (conjugate gradient)或SMO求解,且求解效率通常高於標準SVM的二次凸最佳化問題。研究表明,對任意維度的特徵空間,當樣本間
線性獨立 (linearly independent)時,LS-SVM和SVM會得到相同的結果,若該條件不滿足,則二者的輸出是不同的。一個對二者進行比較的例子是雙螺旋分類(two-spiral classification)。
雙螺旋分類實例,陰影為LS-SVM的分類結果 結構化SVM(structured SVM)
結構化SVM是標準SVM在處理結構化預測(structured prediction)問題時所得到的推廣,給定樣本空間和標籤空間的結構化數據
和標籤空間內的距離函式
,其最佳化問題如下:
結構化SVM被套用於自然語言處理(Natural Language Processing, NLP)問題中,例如給定語料庫數據對其語法分析器(parser)的結構進行預測,也被用於
生物信息學 (bioinformatics)中的
蛋白質結構預測 (protein structure prediction)。
多核SVM(multiple kernel SVM)
多核SVM是多核學習(multiple kernel learning)在監督學習中的實現,是在標準的非線性SVM中將單個核函式替換為核函式族(kernel family)的改進算法。多核SVM的構建方法可以被歸納為以下5類:
顯式規則(fixed rule):在不加入任何超參數的情形下使用核函式的性質,例如線性可加性構建核函式族。顯示規則構建的多核SVM可以直接使用標準SVM的方法進行求解。
啟發式方法(heuristic approach):使用包含參數的組合函式構建核函式族,參數按參與構建的單個核函式的核矩陣或分類表現確定。
最佳化方法(optimization approach):使用包含參數的組合函式構建核函式族,參數按核函式間的相似性或最小化結構風險或所得到的最佳化問題求解。
貝葉斯方法(Bayesian approach):使用包含參數的組合函式構建核函式族,參數被視為隨機變數並按貝葉斯推斷方法進行估計。
提升方法(Boosting approach):按疊代方式不斷在核函式族中加入核函式直到多核SVM的分類表現不再提升為止。
研究表明,從分類的準確性而言,多核SVM具有更高的靈活性,在總體上也優於使用其核函式族中某個單核計算的標準SVM,但非線性和依賴於樣本的核函式族構建方法不總是更優的。核函式族的構建通常依具體問題而定。
擴展算法 支持向量回歸(Support Vector Regression, SVR)
將SVM由分類問題推廣至回歸問題可以得到支持向量回歸(Support Vector Regression, SVR),此時SVM的標準算法也被稱為支持向量分類(Support Vector Classification, SVC)。SVC中的超平面決策邊界是SVR的回歸模型:
。SVR具有稀疏性,若樣本點與回歸模型足夠接近,即落入回歸模型的間隔邊界內,則該樣本不計算損失,對應的損失函式被稱為ε-不敏感損失函式(ε-insensitive loss):
,其中
是決定間隔邊界寬度的超參數。可知,不敏感損失函式與SVC使用的鉸鏈損失函式相似,在原點附近的部分取值被固定為0。類比軟邊距SVM,SVR是如下形式的二次凸最佳化問題:
使用鬆弛變數
表示ε-不敏感損失函式的分段取值後可得:
類似於軟邊距SVM,通過引入
拉格朗日乘子 :
可得到其拉格朗日函式和對偶問題:
SVR可以通過核方法得到非線性的回歸結果。此外LS-SVM可以按與SVR相似的方法求解回歸問題。
支持向量聚類(support vector clustering)
支持向量聚類是一類非參數的
聚類算法 ,是SVM在聚類問題中的推廣。具體地,支持向量聚類首先使用核函式,通常是徑向基函式核,將樣本映射至高維空間,隨後使用SVDD(Support Vector Domain Description)算法得到一個閉合超曲面作為高維空間中樣本點富集區域的刻畫。最後,支持向量聚類將該曲面映射回原特徵空間 ,得到一系列閉合等值線,每個等值線內部的樣本會被賦予一個類別。
使用RBF核和不同超參數的支持向量聚類實例。 支持向量聚類不要求預先給定聚類個數,研究表明,支持向量聚類在低維學習樣本的聚類中有穩定表現,高維樣本通過其它
降維 (dimensionality reduction)方法進行預處理後也可進行支持向量聚類。
半監督SVM(Semi-Supervised SVM, S3VM)
S3VM是SVM在
半監督學習 中的套用,可以套用於少量標籤數據和大量無標籤數據組成的學習樣本。在不考慮未標記樣本時,SVM會求解最大邊距超平面,在考慮無標籤數據後,S3VM會依據低密度分隔(low density separation)假設求解能將兩類標籤樣本分開,且穿過無標籤數據低密度區域的劃分超平面。
S3VM的一般形式是按標準SVM的方法從標籤數據中求解決策邊界,並通過探索無標籤數據對決策邊界進行調整。在軟邊距SVM的基礎上,S3VM的最佳化問題另外引入了2個鬆弛變數:
式中
為有標籤和無標籤樣本的個數,鬆弛變數
表示SSVM將無標籤數據歸入兩個類別產生的經驗風險。
S3VM有很多變體,包括直推式SVM(Transductive SVM, TSVM)、拉普拉斯SVM(Laplacian SVM)和均值S3VM(mean S3VM)。
性質 穩健性與稀疏性:SVM的最佳化問題同時考慮了經驗風險和結構風險最小化,因此具有穩定性。從幾何觀點,SVM的穩定性體現在其構建超平面決策邊界時要求邊距最大,因此間隔邊界之間有充裕的空間包容測試樣本。SVM使用鉸鏈損失函式作為代理損失,鉸鏈損失函式的取值特點使SVM具有稀疏性,即其決策邊界僅由支持向量決定,其餘的樣本點不參與經驗風險最小化。在使用核方法的非線性學習中,SVM的穩健性和稀疏性在確保了可靠求解結果的同時降低了核矩陣的計算量和記憶體開銷。
與其它線性分類器的關係:SVM是一個廣義線性分類器,通過在SVM的算法框架下修改損失函式和最佳化問題可以得到其它類型的線性分類器,例如將SVM的損失函式替換為logistic損失函式就得到了接近於logistic回歸的最佳化問題。SVM和logistic回歸是功能相近的分類器,二者的區別在於logistic回歸的輸出具有機率意義,也容易擴展至多分類問題,而SVM的稀疏性和穩定性使其具有良好的泛化能力並在使用核方法時計算量更小。
作為核方法的性質:SVM不是唯一可以使用核技巧的機器學習算法,
logistic回歸 、
嶺回歸 和
線性判別分析 (Linear DiscriminantAnalysis, LDA)也可通過核方法得到核logistic回歸(kernel logistic regression)、核嶺回歸(kernel ridge regression)和核線性判別分析(Kernelized LDA, KLDA)方法。因此SVM是廣義上核學習的實現之一。
套用 SVM在各領域的模式識別問題中有套用,包括
人像識別 、
文本分類 、手寫字元識別、生物信息學等。
包含SVM的編程模組
基於Python開發的機器學習模組scikit-learn提供預封裝的SVM工具,其設計參考了LIBSVM。其它包含SVM的Python模組有MDP、MLPy、PyMVPA等。
TensorFlow 的高階API組件Estimators有提供SVM的封裝模型。
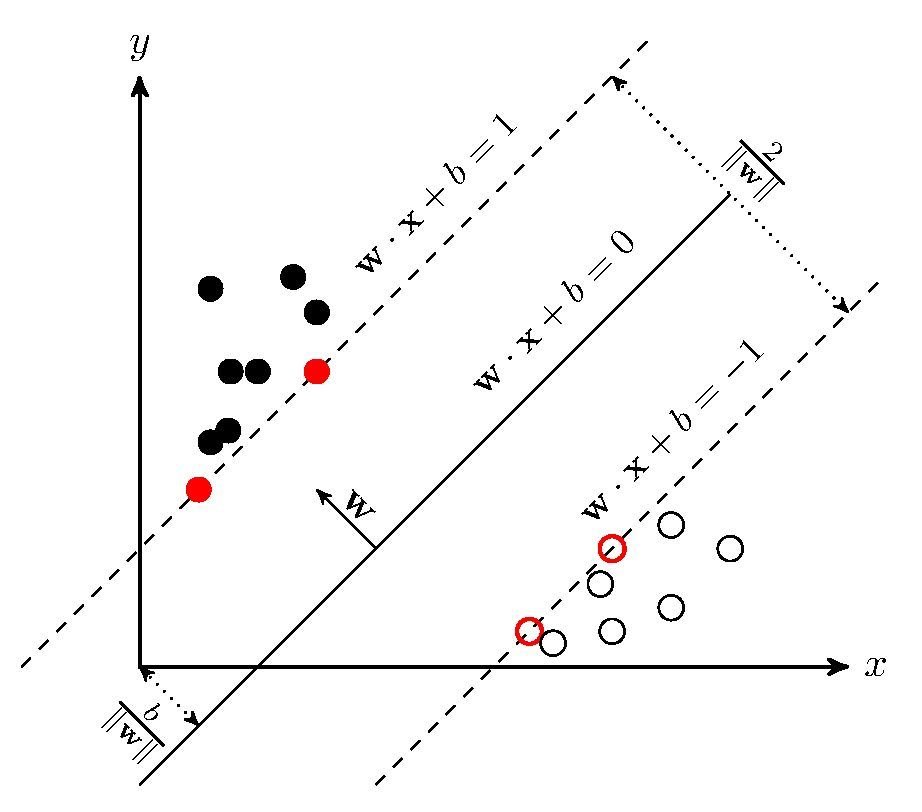 線性可分:決策邊界(實),間隔邊界(虛),支持向量(紅點)
線性可分:決策邊界(實),間隔邊界(虛),支持向量(紅點)




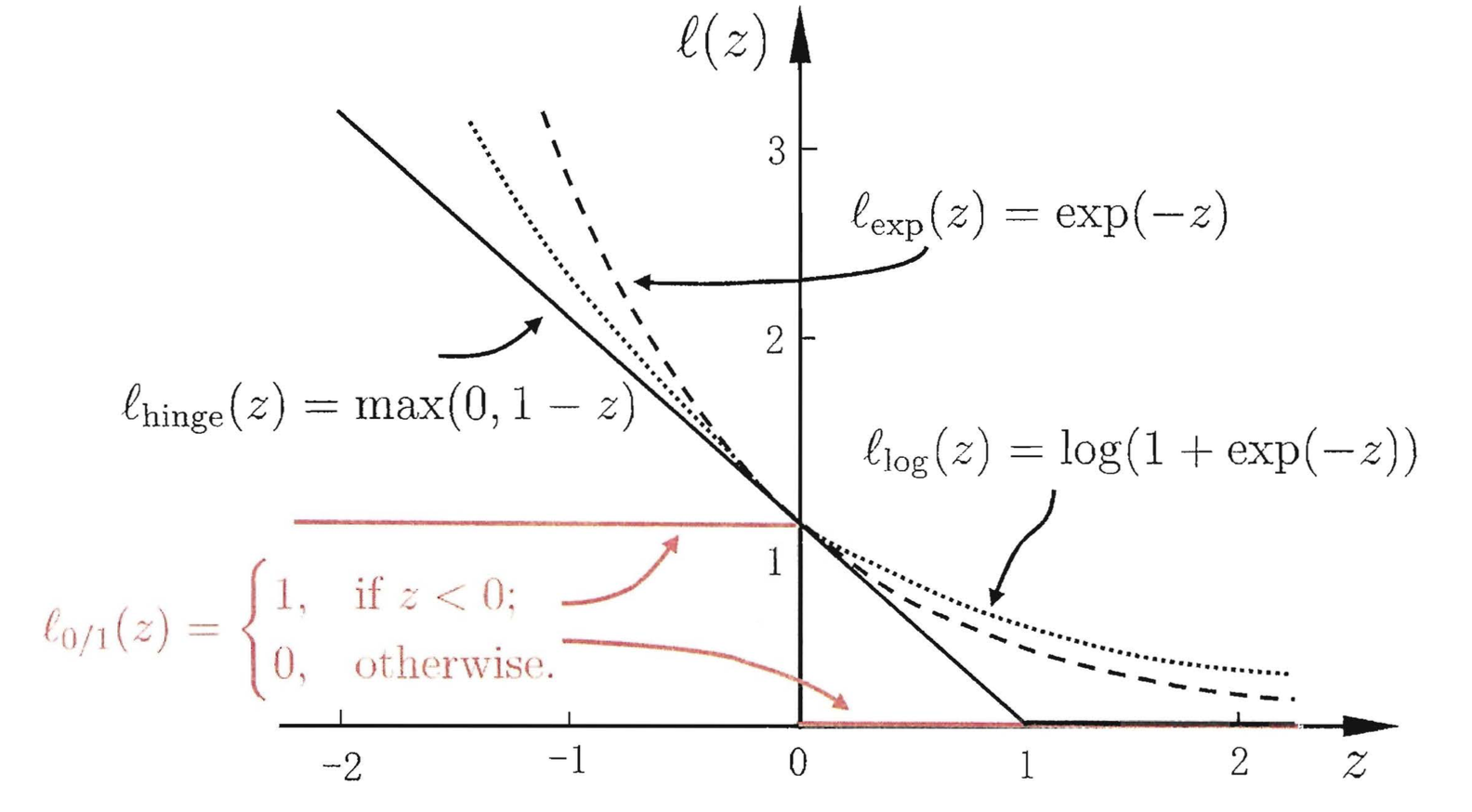 0-1損失函式和其代理損失,紅實線為0-1損失,黑實線為鉸鏈損失。
0-1損失函式和其代理損失,紅實線為0-1損失,黑實線為鉸鏈損失。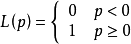



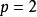


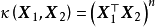



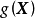
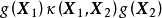





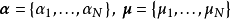




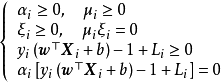



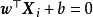
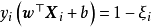














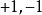
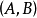
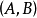





 雙螺旋分類實例,陰影為LS-SVM的分類結果
雙螺旋分類實例,陰影為LS-SVM的分類結果









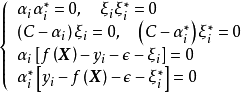

 使用RBF核和不同超參數的支持向量聚類實例。
使用RBF核和不同超參數的支持向量聚類實例。