logistic回歸又稱logistic回歸分析，是一種廣義的線性回歸分析模型，常用於數據挖掘，疾病自動診斷，經濟預測等領域。例如，探討引發疾病的危險因素，並根據危險因素預測疾病發生的機率等。以胃癌病情分析為例，選擇兩組人群，一組是胃癌組，一組是非胃癌組，兩組人群必定具有不同的體徵與生活方式等。因此因變數就為是否胃癌，值為“是”或“否”，自變數就可以包括很多了，如年齡、性別、飲食習慣、幽門螺桿菌感染等。自變數既可以是連續的，也可以是分類的。然後通過logistic回歸分析，可以得到自變數的權重，從而可以大致了解到底哪些因素是胃癌的危險因素。同時根據該權值可以根據危險因素預測一個人患癌症的可能性。
基本介紹
- 中文名：logistic回歸
- 外文名：logistic regressive
- 定義：線性回歸模型
- 分類：計算機 數學
- 用途：預測 判別
- 領域：數據挖掘 疾病診斷 經濟預測
概念,主要用途,尋找危險因素,預測,判別,案例分析,其他信息,
概念
logistic回歸是一種廣義線性回歸（generalized linear model），因此與多重線性回歸分析有很多相同之處。它們的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求參數，其區別在於他們的因變數不同，多重線性回歸直接將w‘x+b作為因變數，即y =w‘x+b，而logistic回歸則通過函式L將w‘x+b對應一個隱狀態p，p =L(w‘x+b),然後根據p 與1-p的大小決定因變數的值。如果L是logistic函式，就是logistic回歸，如果L是多項式函式就是多項式回歸。
logistic回歸的因變數可以是二分類的，也可以是多分類的，但是二分類的更為常用，也更加容易解釋，多類可以使用softmax方法進行處理。實際中最為常用的就是二分類的logistic回歸。
Logistic回歸模型的適用條件
1 因變數為二分類的分類變數或某事件的發生率，並且是數值型變數。但是需要注意，重複計數現象指標不適用於Logistic回歸。
2 殘差和因變數都要服從二項分布。二項分布對應的是分類變數，所以不是常態分配，進而不是用最小二乘法，而是最大似然法來解決方程估計和檢驗問題。
3 自變數和Logistic機率是線性關係
4 各觀測對象間相互獨立。
原理：如果直接將線性回歸的模型扣到Logistic回歸中，會造成方程二邊取值區間不同和普遍的非直線關係。因為Logistic中因變數為二分類變數，某個機率作為方程的因變數估計值取值範圍為0-1，但是，方程右邊取值範圍是無窮大或者無窮小。所以，才引入Logistic回歸。
Logistic回歸實質：發生機率除以沒有發生機率再取對數。就是這個不太繁瑣的變換改變了取值區間的矛盾和因變數自變數間的曲線關係。究其原因，是發生和未發生的機率成為了比值 ，這個比值就是一個緩衝，將取值範圍擴大，再進行對數變換，整個因變數改變。不僅如此，這種變換往往使得因變數和自變數之間呈線性關係，這是根據大量實踐而總結。所以，Logistic回歸從根本上解決因變數要不是連續變數怎么辦的問題。還有，Logistic套用廣泛的原因是許多現實問題跟它的模型吻合。例如一件事情是否發生跟其他數值型自變數的關係。
注意：如果自變數為字元型，就需要進行重新編碼。一般如果自變數有三個水平就非常難對付，所以，如果自變數有更多水平就太複雜。這裡只討論自變數只有三個水平。非常麻煩，需要再設二個新變數。共有三個變數，第一個變數編碼1為高水平，其他水平為0。第二個變數編碼1為中間水平，0為其他水平。第三個變數，所有水平都為0。實在是麻煩，而且不容易理解。最好不要這樣做，也就是，最好自變數都為連續變數。
spss操作：進入Logistic回歸主對話框，通用操作不贅述。
發現沒有自變數這個說法，只有協變數，其實協變數就是自變數。旁邊的塊就是可以設定很多模型。
“方法”欄：這個根據詞語理解不容易明白，需要說明。
共有7種方法。但是都是有規律可尋的。
“向前”和“向後”：向前是事先用一步一步的方法篩選自變數，也就是先設立門檻。稱作“前”。而向後，是先把所有的自變數都進來，然後再篩選自變數。也就是先不設定門檻，等進來了再一個一個淘汰。
“LR”和“Wald”,LR指的是極大偏似然估計的似然比統計量機率值，有一點長。但是其中重要的詞語就是似然。
Wald指Wald統計量機率值。
“條件”指條件參數似然比統計量機率值。
“進入”就是所有自變數都進來，不進行任何篩選
將所有的關鍵字組合在一起就是7種方法，分別是“進入”“向前LR”“向前Wald”"向後LR"“向後Wald”“向後條件”“向前條件”
下一步：一旦選定協變數，也就是自變數，“分類”按鈕就會被激活。其中，當選擇完分類協變數以後，“更改對比”選項組就會被激活。一共有7種更改對比的方法。
“指示符”和“偏差”，都是選擇最後一個和第一個個案作為對比標準，也就是這二種方法能夠激活“參考類別”欄。“指示符”是默認選項。“偏差”表示分類變數每個水平和總平均值進行對比，總平均值的上下界就是"最後一個"和"第一個"在“參考類別”的設定。
“簡單”也能激活“參考類別”設定。表示對分類變數各個水平和第一個水平或者最後一個水平的均值進行比較。
“差值”對分類變數各個水平都和前面的水平進行作差比較。第一個水平除外，因為不能作差。
“Helmert”跟“差值”正好相反。是每一個水平和後面水平進行作差比較。最後一個水平除外。仍然是因為不能做差。
“重複”表示對分類變數各個水平進行重複對比。
“多項式”對每一個水平按分類變數順序進行趨勢分析，常用的趨勢分析方法有線性，二次式。
主要用途
尋找危險因素
正如上面所說的尋找某一疾病的危險因素等。
預測
判別
實際上跟預測有些類似，也是根據logistic模型，判斷某人屬於某病或屬於某種情況的機率有多大，也就是看一下這個人有多大的可能性是屬於某病。
這是logistic回歸最常用的三個用途，實際中的logistic回歸用途是極為廣泛的，logistic回歸幾乎已經成了流行病學和醫學中最常用的分析方法，因為它與多重線性回歸相比有很多的優勢，以後會對該方法進行詳細的闡述。實際上有很多其他分類方法，只不過Logistic回歸是最成功也是套用最廣的。
案例分析
關於富士康跳樓曲線的Logistic回歸分析。
首先找出所有富士康員工自殺的日期：
列出如下表格：（以07年6月18號，第一例自殺案例為原點，至今（10年5月25日）1072天）
自殺時間x/d | 0 | 75 | 272 | 758 | 794 | 950 | 997 | 1003 | 1015 |
1023 | 1024 | 1024 | 1053 | 1051 | 1072 |
累計自殺人數y | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
10 | 11 | 12 | 13 | 14 | 15 |
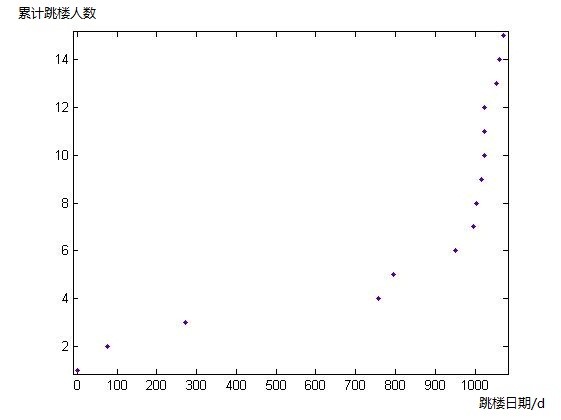
在MATLAB中容易做出散點圖：
可見這是一個指數增長的曲線。
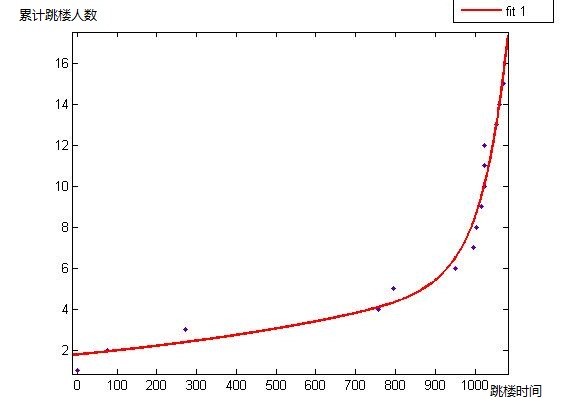
其增長曲線與對數增長很接近。
General model Exp2:
f(x) = a*exp(b*x) + c*exp(d*x)
Coefficients (with 95% confidence bounds):
a = 7.569e-007 (-6.561e-006, 8.075e-006)
b = 0.01529 (0.006473, 0.0241)
c = 1.782 (0.5788, 2.984)
d = 0.001075 (2.37e-005, 0.002125)
Goodness of fit:
SSE: 8.846
R-square: 0.9684
Adjusted R-square: 0.9598
RMSE: 0.8968
可見相關度0.96也是非常高的。
然而和所有疾病一樣，一旦其事件引起了人們的關注，則各方的反饋作用，將阻礙其繼續上升。
因此，和很多流行病分析一樣，該曲線很有可能呈S型。對於該曲線的分析，使用Logistic回歸。
首先假設Logis(B,x)=F(x),之中B為參數數組，則由經驗和可能的微分方程關係，回歸曲線應該為
S（x）=m*Logis（B,x+t）/（n+Logis（B,x+t））格式
由於當Logis（B,x）較小時S(x)=Logis（B,x），則可以認為f（x）的參數可以直接引入S（x）作為一種近似，而對於m，n的確定，以1為間隔，畫出m*n=40*20的所有曲線，
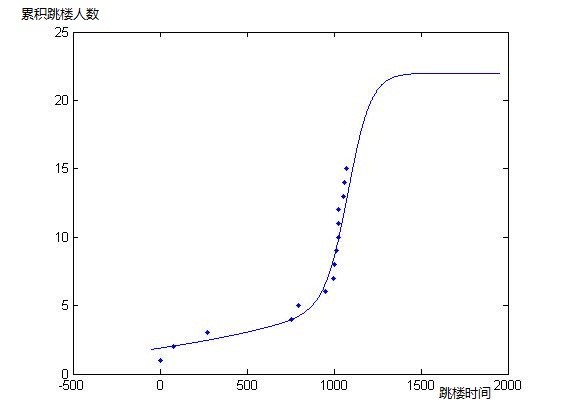
選出其中最吻合的的一條（m=22 n=20 t=50）：
其他信息
由此可以見，富士康的跳樓人數最終會穩定在在22人左右，仍然不會超過全國平均跳樓率。
對此曲線的分析，借鑑微生物生長曲線的方法，將其分為：
緩慢期，富士康員工雖然受到很大的工作壓力，可是其自身的心理並沒有崩潰，因此跳樓這種事件發生頻率很少，而且呈線性關係，說明沒有跳樓者受到別的跳樓者的影響。
對數期，富士康員工由於受到工廠巨大的工作壓力，以及來自社會各方的壓力，甚至加上上級的欺壓，心理防線漸漸崩潰，無處發泄。而一旦有想不開者跳樓，則為其提供了一個發泄的模板，這種情況下，很容易有相同經歷的員工受到跳樓者的影響，從而一個接一個的跳樓自殺。目前的富士康正處於此時期。
穩定期，由於社會、媒體各方面的關注以及社會、廣大人民對工廠的壓力，工廠不得不做出改變，員工的心理壓力漸漸得到釋放，從而員工跳樓輕生頻率會很快下降。
