基本介紹
- 中文名:多重線性回歸
- 外文名:multiple linear regression
- 簡稱:多重回歸
- 所屬學科:數學
- 相關概念:偏回歸係數,殘差,多重共線性等
基本信息

















參數估計

假設檢驗

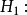













自變數的選擇



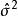

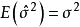


























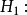
















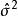

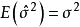






多重線性回歸(multiple linear regression) 是簡單直線回歸的推廣,研究一個因變數與多個自變數之間的數量依存關係。多重線性回歸用回歸方程描述一個因變數與多個...
SPSS統計分析過程包括描述性統計、均值比較、一般線性模型、相關分析、回歸分析、對數線性模型、聚類分析、數據簡化、生存分析、時間序列分析、多重回響等幾大類,每類...
多元線性回歸模型,(multivariable linear regression model )在實際經濟問題中,一個變數往往受到多個變數的影響。例如,家庭消費支出,除了受家庭可支配收入的影響外,還...
多重共線性是指線性回歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。一般來說,由於經濟數據的限制使得模型設計不當,導致...
一元線性回歸是一個主要影響因素作為自變數來解釋因變數的變化,在現實問題研究中...兩個以上的影響因素作為自變數來解釋因變數的變化,這就是多元回歸亦稱多重回歸。...
多重判定係數是多元回歸中的回歸平方和占總平方和的比例,它是度量多元回歸方程擬合程度的一個統計量,反映了在因變數y的變差中被估計的回歸方程所解釋的比例。...
回歸分析按照涉及的變數的多少,分為一元回歸和多元回歸分析;按照因變數的多少,可分為簡單回歸分析和多重回歸分析;按照自變數和因變數之間的關係類型,可分為線性回歸...
線性回歸方程是利用數理統計中的回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法之一。線性回歸也是回歸分析中第一種經過嚴格研究並在實際...
多元回歸分析(Multiple Regression Analysis)是指在相關變數中將一個變數視為因變數,其他一個或多個變數視為自變數,建立多個變數之間線性或非線性數學模型數量關係式...
多重線性等價(mufti-linear equivalent)是具有相同多重線性恆等式的代數類。代數學是數學中一個重要的、基礎的分支。代數學一般分為初等代數學(或稱古典代數學)和...
線性回歸分析是根據一個或一組自變數的變動情況預測與其相關關係的某隨機變數的未來值的一種方法。回歸分析需要建立描述變數間相關關係的回歸方程。根據自變數的個數,...
回歸模型(regression model)對統計關係進行定量描述的一種數學模型。如多元線性回歸的數學模型可以表示為y=β0+β1*x+εi,式中,β0,β1,…,βp是p+1個待...
研究一個因變數、與兩個或兩個以上自變數的回歸。亦稱為多元線性回歸,是反映一種現象或事物的數量依多種現象或事物的數量的變動而相應地變動的規律。建立多個變數...
偏回歸係數是多元回歸問題出現的一個特殊性質。設自變數x1,x2,…,xm與因變數y都具有線性關係,可建立回歸方程:ŷ=b0+b1x1+b2x2+…+bmxm。式中b1,b2,…,...
logistic回歸又稱logistic回歸分析,是一種廣義的線性回歸分析模型,常用於數據挖掘,疾病自動診斷,經濟預測等領域。例如,探討引發疾病的危險因素,並根據危險因素預測疾病...
主成分回歸分析(principle component regression;PCR),以主成分為自變數進行的回歸分析。是分析多元共線性問題的一種方法。用主成分得到的回歸關係不像用原自變數建立...
這是最常用的模型,稱為多重線性回歸或多元線性回歸。用樣本估計線性回歸模型中未知常數的方法也很多,經典的方法為最小二乘法,它的理論較為完善,此法較適用於回歸...
在多元線性回歸模型中,各個解釋變數之間不能存線上性相關關係。如果一個解釋變數與其他解釋變數之間存在著線性相關關係,則稱該模型具有“多重共線性”。這將影響對...
