偏回歸係數是多元回歸問題出現的一個特殊性質。設自變數x1,x2,…,xm與因變數y都具有線性關係,可建立回歸方程:ŷ=b0+b1x1+b2x2+…+bmxm。式中b1,b2,…,bm為相應於各自變數的偏回歸係數。表示當其他的各自變數都保持一定時,指定的某一自變數每變動一個單位,因變數y增加或減少的數值。
基本介紹
概念解釋
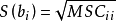
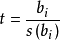
介紹
問答
標準化偏回歸係數



偏回歸係數是多元回歸問題出現的一個特殊性質。設自變數x1,x2,…,xm與因變數y都具有線性關係,可建立回歸方程:ŷ=b0+b1x1+b2x2+…+bmxm。式中b1,b2,…,bm為相應於各自變數的偏回歸係數。表示當其他的各自變數都保持一定時,指定的某一自變數每變動一個單位,因變數y增加或減少的數值。
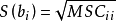
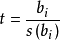


偏回歸係數是多元回歸問題出現的一個特殊性質。設自變數x1,x2,…,xm與因變數y都具有線性關係,可建立回歸方程:ŷ=b0+b1x1+b2x2+…+bmxm。式中b1,b2,…,...
1 根據上面的說法,從線性回歸的角度計算變數間的偏相關係數,但是這樣做很麻煩。2 疊代法,可以認為簡單相關係數為0階偏相關係數,任何n階偏相關都可以通過3個(n-...
線上性回歸中引入新自變數後,所減少的殘差平方和與該自變數引入前的殘差平方和之比稱為因變數與新引入的自變數之間的偏判定係數,其數值等於相應樣本偏相關係數的平方...
偏回歸係數的標準誤 [1] 。多重線性回歸自變數的選擇 編輯 在許多多重線性回歸中,模型中包含的自變數沒有辦法事先確定,如果把一些不重要的或者對因變數影響很弱...
βj也被稱為偏回歸係數(partial regression coefficient)多元線性回歸模型計算模型 編輯 一元線性回歸是一個主要影響因素作為自變數來解釋因變數的變化,在現實問題研究...
這一假定是建立Cox回歸模型的前提條件。2.對數線性假定 模型中的協變數應與對數風險比呈線性關係,如公式(2)。Cox回歸模型中偏回歸係數的意義...
固定時,x1每增加一個單位對y的效應,即x1對y的偏回歸係數;同理b2為x1,xk固定時,x2每增加一個單位對y的效應,即,x2對y的偏回歸係數,等等。如果兩個自變數x1...
普通偏殘差圖對自變數在回歸方程中函式形式的提示作用[J]. 醫學爭鳴, 1998(3):254-256. 3. 劉連福. 一元線性回歸方程中回歸係數的幾種確定方法[J]. 瀋陽...
《回歸分析:因變數統計模型》旨在為用模型法對因變數做智慧型分析提供必須的工具。...3.7 多元回歸因變數推論 3.8 相關和決定係數 多重相關偏相關 3.9 求得...
方差膨脹係數(variance inflation factor,VIF)是衡量多元線性回歸模型中復 (多重)共線性嚴重程度的一種度量。它表示回歸係數估計量的方差與假設自變數間不線性相關時...
之間確有線性關係,在求解回歸方程前,線性回歸模型只是一種假設,所以在求出線性回歸方程之後,還需對其進行統計檢驗,給以肯定或否定的結論。有關回歸方程及回歸係數的...
它通過構造一個懲罰函式得到一個較為精煉的模型,使得它壓縮一些回歸係數,即強制...因此保留了子集收縮的優點,是一種處理具有復共線性數據的有偏估計。...
計算變數 ,相應的回歸係數的 F 檢驗統計量的值,記為 ,取其中的最大值 ,即...逐步回歸分析的實施過程是每一步都要對已引入回歸方程的變數計算其偏回歸平方和...
嶺回歸(英文名:ridge regression, Tikhonov regularization)是一種專用於共線性數據分析的有偏估計回歸方法,實質上是一種改良的最小二乘估計法,通過放棄最小二乘法...
偏自相關函式是描述隨機過程結構特徵的一種方法。用Φkj表示k階自回歸式中第j個回歸係數,則k階自回歸模型表示為xt=Φk1xt-1+Φk2xt-2+...+Φkkxt-k+ut...
其次,如果y與m個自變數總的來說有線性關係,也並不意味著所有自變數都與因變數有線性關係,還需對每個自變數的偏回歸係數進行t檢驗,以剔除在方程中不起作用的自變數...
