基本介紹
原理
運算案例
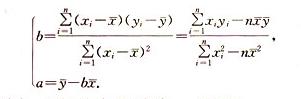 最小二乘法求回歸直線方程中a、b的公式
最小二乘法求回歸直線方程中a、b的公式
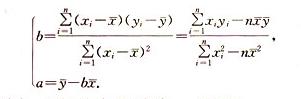 最小二乘法求回歸直線方程中a、b的公式
最小二乘法求回歸直線方程中a、b的公式回歸方程是根據樣本資料通過回歸分析所得到的反映一個變數(因變數)對另一個或一組變數(自變數)的回歸關係的數學表達式。回歸直線方程用得比較多,可以用最小二乘法...
線性回歸方程是利用數理統計中的回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法之一。線性回歸也是回歸分析中第一種經過嚴格研究並在實際...
回歸直線方程指在一組具有相關關係的變數的數據(x與Y)間,一條最好地反映x與y之間的關係直線。離差作為表示Xi對應的回歸直線縱坐標y與觀察值Yi的差,其幾何意義...
回歸,指研究一組隨機變數(Y1 ,Y2 ,…,Yi)和另一組(X1,X2,…,Xk)變數之間關係的統計分析方法,又稱多重回歸分析。通常Y1,Y2,…,Yi是因變數,X1、X2,…...
回歸分析只涉及到兩個變數的,稱一元回歸分析。一元回歸的主要任務是從兩個相關變數中的一個變數去估計另一個變數,被估計的變數,稱因變數,可設為Y;估計出的...
方程回歸是指根據樣本資料通過回歸分析所得到的反映一個變數(因變數)對另一個或一組變數(自變數)的回歸關係的數學表達式。回歸直線方程用得比較多,可以用最小二乘...
回歸模型(regression model)對統計關係進行定量描述的一種數學模型。如多元線性回歸的數學模型可以表示為y=β0+β1*x+εi,式中,β0,β1,…,βp是p+1個待...
線性回歸是利用數理統計中回歸分析,來確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法,運用十分廣泛。其表達形式為y = w'x+e,e為誤差服從均值為0...
回歸分析(regression analysis)是確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法。運用十分廣泛,回歸分析按照涉及的變數的多少,分為一元回歸和多元回歸...
回歸係數(regression coefficient)在回歸方程中表示自變數x 對因變數y 影響大小的參數。回歸係數越大表示x 對y 影響越大,正回歸係數表示y 隨x 增大而增大,負回歸...
回歸方程式是一個數學名詞。...... 自Doust等人在50年代末進行漁船阻力回歸以來,隨著電子計算機的廣泛套用,這項工作也隨之在一些國家與有關部門展開,但所回歸出的方...
研究一個因變數、與兩個或兩個以上自變數的回歸。亦稱為多元線性回歸,是反映一種現象或事物的數量依多種現象或事物的數量的變動而相應地變動的規律。建立多個變數...
回歸分析法指利用數據統計原理,對大量統計數據進行數學處理,並確定因變數與某些自變數的相關關係,建立一個相關性較好的回歸方程(函式表達式),並加以外推,用於預測...
提到回歸直線,首先要知道變數的相關性。變數與變數之間的關係常見的有兩類:一類是確定性的函式關係,像正方形的邊長a和面積S的關係;另一類是變數間確實存在關係,但...
在統計學中,線性回歸是利用稱為線性回歸方程的最小二乘函式對一個或多個自變數和因變數之間關係進行建模的一種回歸分析。這種函式是一個或多個稱為回歸係數的模型...
多重線性回歸(multiple linear regression) 是簡單直線回歸的推廣,研究一個因變數與多個自變數之間的數量依存關係。多重線性回歸用回歸方程描述一個因變數與多個...
曲線回歸(curvilinear regression)是指對於非線性關係的變數進行回歸分析的方法。曲線回歸方程一般是以自變數的多項式表達因變數。方法是:根據數據的特點先進行某些變換(...
在回歸分析中,如果有兩個或兩個以上的自變數,就稱為多元回歸。事實上,一種現象常常是與多個因素相聯繫的,由多個自變數的最優組合共同來預測或估計因變數,比只用...
多元線性回歸模型,(multivariable linear regression model )在實際經濟問題中,一個變數往往受到多個變數的影響。例如,家庭消費支出,除了受家庭可支配收入的影響外,還...
