基本介紹
- 中文名:多重共線性
- 外文名:Multicollinearity
- 相關詞目:近似共線性
- 依據模型:線性回歸模型
簡介
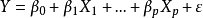
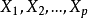
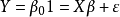


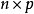
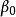
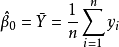
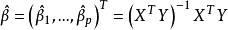
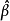
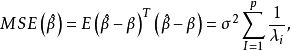
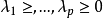
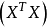
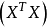

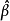
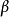
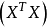
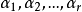
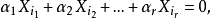
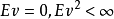
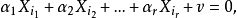
產生原因
影響
判斷方法

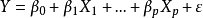
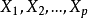
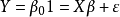


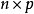
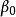
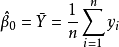
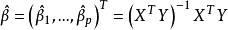
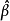
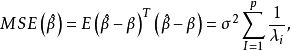
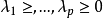
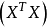
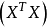

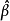
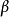
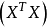
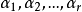
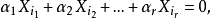
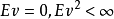
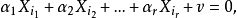

多重共線性是指線性回歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。一般來說,由於經濟數據的限制使得模型設計不當,導致...
多重線性回歸(multiple linear regression) 是簡單直線回歸的推廣,研究一個因變數與多個自變數之間的數量依存關係。多重線性回歸用回歸方程描述一個因變數與多個...
是共線的,對於觀察變數,我們有:這意味著如果將各種觀察 繪製在 平面中,這些點在本文前面定義的意義上是共線的。多重共線性是指多重回歸模型中k(k≥2)個解釋...
是共線的,對於觀察變數,我們有:這意味著如果將各種觀察 繪製在 平面中,這些點在本文前面定義的意義上是共線的。多重共線性是指多重回歸模型中k(k≥2)個解釋...
也可能是自變數之間有共線性所致,此時應設法降低共線性的影響。多重共線性是指在多元線性回歸方程中,自變數之間有較強的線性關係,這種關係若超過了因變數與自變數的...
共線性,即同線性或同線型。統計學中,共線性即多重共線性。多重共線性(Multicollinearity)是指線性回歸模型中的解釋變數之間由於存在精確相關關係或高度相關關係而使...
層次分析法線上性回歸方程中的套用[J]. 四川理工學院學報(自然科學版),2006,05:99-101. 3. [2]馬雄威. 線性回歸方程中多重共線性診斷方法及其實證分析[J]....
在多元線性回歸模型中,各個解釋變數之間不能存線上性相關關係。如果一個解釋變數與其他解釋變數之間存在著線性相關關係,則稱該模型具有“多重共線性”。這將影響對...
方差膨脹因子(Variance Inflation Factor,VIF):是指解釋變數之間存在多重共線性時的方差與不存在多重共線性時的方差之比。容忍度的倒數,VIF越大,顯示共線性越嚴重...
風訊VIF(foosun Vif)是VIF與四川風訊科技有限公司聯合推出的一款多功能的IIS防護...經驗判斷方法表明:當0<VIF<10,不存在多重共線性;當10≤VIF<100,存在較強的...
方差擴大因子(variance inflation factor)簡稱VIF,是表征自變數觀察值之間復共線性程度的數值。線性回歸分析中,回歸係數βj的估計量的方差為σ2Cjj,其中Cjj=(1-Rj)...
回歸分析按照涉及的變數的多少,分為一元回歸和多元回歸分析;按照因變數的多少,可分為簡單回歸分析和多重回歸分析;按照自變數和因變數之間的關係類型,可分為線性回歸...
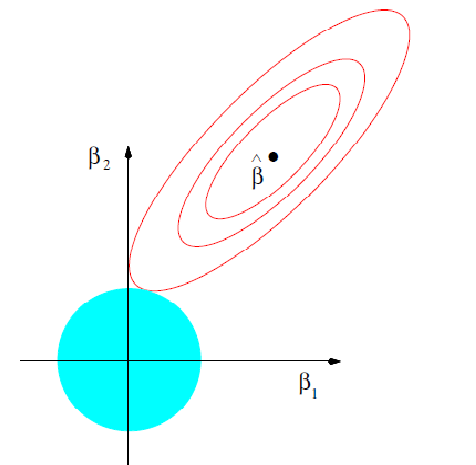
嶺回歸分析是一種用於存在多重共線性(自變數高度相關)數據的技術。在多重共線性情況下,儘管最小二乘法(OLS)對每個變數很公平,但它們的差異很大,使得觀測值偏移並...
[5]吳相波 葉阿忠.局部線性估計中的多重共線性問題[J].統計與決策.2007,(4).[6] Azhong Ye, Rob J Hyndman and Zinai Li. Local linear multivariate ...
依據上述思想,可利用逐步回歸篩選並剔除引起多重共線性的變數,其具體步驟如下:先用被解釋變數對每一個所考慮的解釋變數做簡單回歸,然後以對被解釋變數貢獻最大的解...
方差膨脹係數(variance inflation factor,VIF)是衡量多元線性回歸模型中復 (多重)共線性嚴重程度的一種度量。它表示回歸係數估計量的方差與假設自變數間不線性相關時...
第12章介紹區間估計的基本理論,第13章介紹方差分析,第14章介紹回歸分析的基本理論,第15章介紹回歸分析的高級理論與套用(包括結構突變的檢驗、分塊回歸、多重共線性...
社會經濟制度之間存在著極為複雜的相互作用機制,而運用數學計量工具可以將有關影響因素予以固定,從而把握複雜現象之間的內在聯繫,消除變數內生性、異方差和多重共線性...
局部線性估計和變窗寬局部線性估計、非參數計量經濟模型的異方差問題和多重共線性問題;第三部分為非參數計量經濟聯立方程模型,包括非參數計量經濟聯立模型的局部線性...
面板數據分析方法是最近幾十年來發展起來的新的統計方法,面板數據可以克服時間序列分析受多重共線性的困擾,能夠提供更多的信息、更多的變化、更少共線性、更多的...
進行多重共線性檢驗,去除與其他指標存在多重共線性的指標;第三步,進行KMO檢驗,確定是否進行因子分析;第四步,進行Logistic回歸,得到模型,觀察模型擬合程度及預測準確...
