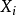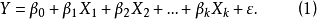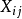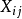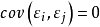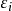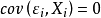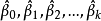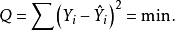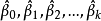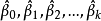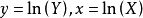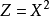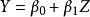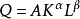多元回歸分析

多元回歸分析(Multiple Regression Analysis)是指在相關變數中將一個變數視為因變數，其他一個或多個變數視為自變數，建立多個變數之間線性或非線性數學模型數量關係式並利用樣本數據進行分析的統計分析方法。另外也有討論多個自變數與多個因變數的線性依賴關係的多元回歸分析，稱為多元多重回歸分析模型(或簡稱多對多回歸)。

基本介紹

• 中文名：多元回歸分析
• 外文名：Multiple Regression Analysis；multivariate regression analysis
• 別稱：多重回歸、多元回歸等
• 所屬學科：數學（統計學）
• 分類：線性回歸，曲線回歸等
• 相關概念：線性模型，虛擬變數等

基本介紹

通常影響因變數的因素有多個，這種多個自變數影響一個因變數的問題可以通過多元回歸分析來解決。例如，經濟學知識告訴我們，商品需求量Q除了與商品價格P有關外，還受到替代品的價格、互補品的價格，和消費者收入等因素，甚至還包括商品品牌Brand這一品質變數(品質變數不能用數字來衡量，需要在模型中引入虛擬變數)的影響。多元回歸分析套用的範圍更加廣泛。由於線性回歸分析比較簡單和普遍，下面首先介紹多元線性回歸，線上性分析基礎上，逐步引入虛擬變數回歸和一類能夠變換成線性回歸的曲線回歸模型。

多元回歸模型

多元回歸模型的數學形式

設因變數為Y，影響因變數的k個自變數分別為 ，假設每一個自變數對因變數Y的影響都是線性的，也就是說，在其他自變數不變的情況下，Y的均值隨著自變數 的變化均勻變化，這時我們把

稱為總體回歸模型，把 稱為回歸參數。回歸分析的基本任務是：

任務1：利用樣本數據對模型參數作出估計。

任務2：對模型參數進行假設檢驗。

任務3：套用回歸模型對因變數(被解釋變數)作出預測。

模型的基本假定

為了保證多元回歸分析的參數估計、統計檢驗以及置信區間估計的有效性，與一元線性回歸分析類似，我們需要對總體回歸模型及數據作一些基本假定。

假定1：隨機誤差項 的機率分布具有零均值，即 。

假定2：隨機誤差項 的機率分布對於不同的自變數表現值而言，具有同方差。即 的方差不隨著 的變化而變化， 。

假定2：隨機誤差項 的機率分布對於不同的自變數表現值而言，具有同方方差不隨著 的變化而變化， 。

假定3：隨機誤差項 不存在自相關，即 。

假定4： 與任一解釋變數 不相關，可以表示為 。

假定5：解釋變數X之間不存在完全共線性。

以上假定1~4與一元回歸分析的假定是相同的。假定5 是針對解釋變數而言，在一元回歸分析中，由於只有一個解釋變數，因此這一點是不需要的。在模型和數據滿足上述假定時，對式(1)兩邊取期望，可得到：

式(2)稱為總體回歸方程(Population Regression Equation，PRE )或總體回歸函式(Population Regression Function，PRF)， 表示在給定自變數 的條件下觀察值Y的條件均值。在實際問題中，總體參數 往往是未知的，我們需要根據樣本觀察值給出總體參數的相應的估計值 ，此時，

稱為樣本回歸方程(Sample Regression Equation，SRE) 或樣本回歸函式(Sample RegressionFunction，SRF)， 也就是 的點估計值。

多元線性回歸方程的估計

對於多元回歸方程，在模型和數據滿足前文所述的基本假定的前提下，參數估計可以通過最小二乘估計來得到，同樣假設

即

根據高等數學知識，Q分別對 對求偏導數，令其等於0，得到

求解式(5)中的方程組，即可得到參數的估計值 。由於手工計算比較繁瑣，而現在的統計軟體都提供了回歸分析工具，尤其Excel中的回歸分析工具相當簡單。

引進虛擬變數的回歸分析

前面介紹的回歸分析中的自變數和因變數都是數值型變數，如果在回歸分析中引入虛擬變數(分類變數)，則會使模型的套用範圍迅速擴大。在自變數中引入虛擬變數本身並不影響回歸模型的基本假定，因為經典回歸分析是在給定自變數X的條件下被解釋變數Y的隨機分布。但是如果因變數為分類變數，則會改變經典回歸分析的基本假定，一般在計量經濟學教材中有比較深入的介紹，如Logistics回歸等。

當虛擬變數的引入形式只影響回歸方程的截距，我們稱為加法模型。引入虛擬變數的另外一種形式是乘法模型，這時引入虛擬變數後並不影響模型的截距，而是影響了斜率。當然，在模型設定時也可能同時引入加法和乘法，同時改變模型的截距和斜率。

曲線回歸

前面我們在模型中都假定Y和之間是線性關係，從廣義的線性角度來講，下面所講的曲線模型是通過變數替換而轉化成線性的模型。表1列出了常用的可以通過變數替換而轉化成線性的曲線模型。

表1 可以轉化成線性模型的曲線

曲線模型	變數替代	線性模型