在具有兩個類的統計分類問題中,決策邊界或決策表面是超曲面,其將基礎向量空間劃分為兩個集合,一個集合。 分類器將決策邊界一側的所有點分類為屬於一個類,而將另一側的所有點分類為屬於另一個類。
基本介紹
- 中文名:決策邊界
- 外文名:Decision boundary
介紹,在神經網路和支持向量模型中,線性可分集的決策邊界,
介紹
決策邊界是問題空間的區域,分類器的輸出標籤是模糊的。如果決策表面是超平面,那么分類問題是線性的,並且類是線性可分的。
決策界限並不總是明確的。 也就是說,從特徵空間中的一個類到另一個類的過渡不是不連續的,而是漸進的。 這種效果在基於模糊邏輯的分類算法中很常見,其中一個類或另一個類的成員資格是不明確的。
在神經網路和支持向量模型中
在基於反向傳播的人工神經網路或感知器的情況下,網路可以學習的決策邊界的類型由網路具有的隱藏層的數量來確定。如果它沒有隱藏層,那么它只能學習線性問題。如果它有一個隱藏層,則它可以學習Rn的緊緻子集上的任何連續函式,如通用近似定理所示,因此它可以具有任意的決策邊界。
特別地,支持向量機找到超平面,其將特徵空間分成具有最大餘量的兩個類。如果問題最初不是線性可分的,則通過增加維數來使用核心技巧將其轉換為線性可分的問題。因此,小尺寸空間中的一般超曲面在具有更大尺寸的空間中變成超平面。
神經網路試圖學習決策邊界,最小化經驗誤差,而支持向量機試圖學習決策邊界,最大化決策邊界和數據點之間的經驗邊際。
線性可分集的決策邊界
與Logistuc Regression相比,SVM是一種最佳化的分類算法,其動機是尋找一個最佳的決策邊界,使得從決策邊界與各組數據之間存在margin,並且需要使各側的margin最大化。比較容易理解的是,從決策邊界到各個training example的距離越大,在分類操作的差錯率就會越小。因此,SVM也叫作Large Margin Classifier。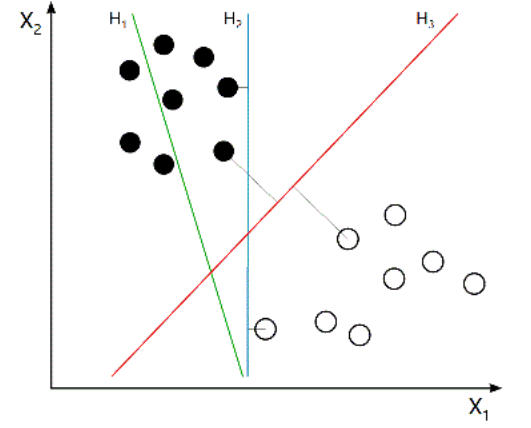 圖1
圖1
 圖1
圖1最簡單的情況是,在二維平面中的,線性可分情況,即我們的training set可以用一條直線來分割稱為兩個子集,如下圖所示。而在圖中我們可以看到,H2和H3都可以正確的將training set進行分類,但細細想來,使用H2進行分類的話,我們對於靠近藍線的幾個訓練樣例其實是不敢說100%的,但對於離藍線最遠的小球,我們卻很有把握。這也是H3這條SVM紅線出現的原因:儘量讓兩側的訓練樣例遠離決策邊界,從而讓我們的分類系統有把握對每個球Say Absolutely。
