求和項是超幾何項的級數稱為超幾何級數。超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。
基本介紹
- 中文名:超幾何級數
- 外文名:hypergeometric series
- 適用範圍:數理科學
- 定義:超幾何方程在單位圓內的第一解
定義




超幾何項

雙超幾何項

正則超幾何項






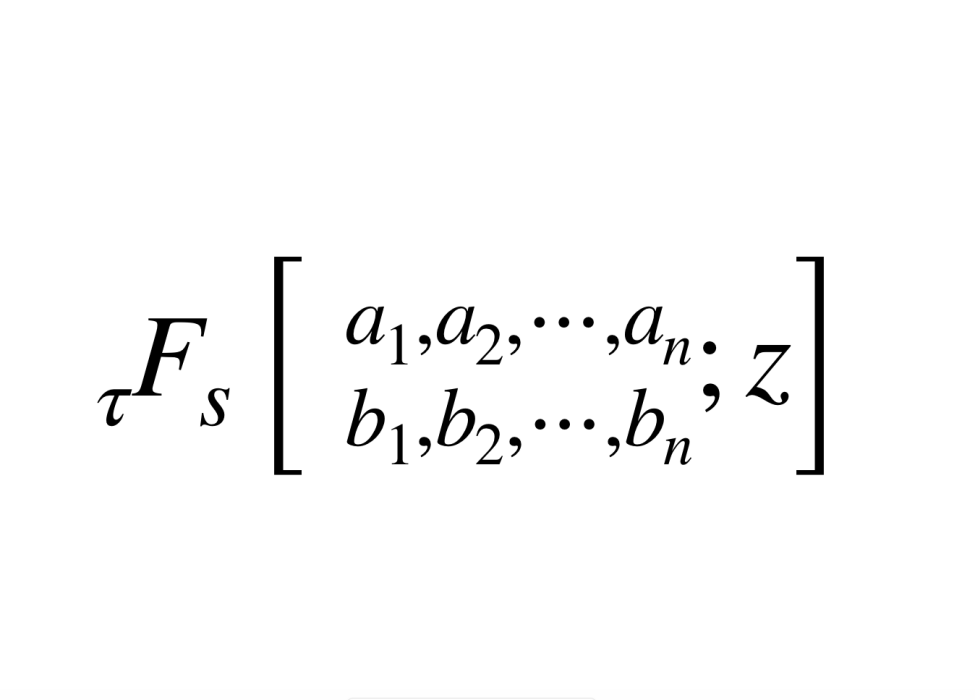
求和項是超幾何項的級數稱為超幾何級數。超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。












求和項是超幾何項的級數稱為超幾何級數。超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。定義超幾何級數亦稱高斯級數,是超幾何方程在單位圓內的第一解。求和項是超幾何項的級數稱為超幾何級數,常用如下記號表示其中且表示升...
超幾何級數 當 c不是0,-1,-2...時,對於|z| 其中 是Pochhammer符號,定義為:當a或b是0或負整數時級數只有有限項。對於滿足|z|≥1 的複數z,超幾何函式可以通過將上述在單位圓內定義的函式沿著避開支點0和1的任意路徑做解析...
廣義超幾何級數 [1](generalized hypergeometricseries)超幾何級數在更多參量情形下的另一種推廣。 中文名 廣義超幾何級數 外文名 generalized hypergeometricseries 廣義超幾何級數即 當pq+1時,除非它截斷為多項式(a aZ,a,中至少有一個...
托瑪級數 托瑪級數,數學名詞。托瑪級數(Thomae series )多參量情形下的一種推廣.(Thomae,L. J.)提出,定義為 其中A為常數.超幾何級數是托瑪級數的特殊情形(m=2,n=1).
超幾何級數是組合數學的一個非常重要的研究分支,文獻中已經有不少有趣的研究成果。同餘式問題和超同餘式問題是數論的一個重要研究課題。 本項目是要利用超幾何級數和q-級數理論的一些結果, 如Chu-Vandermonde恆等式,Pfaff-Saalschutz...
《橢圓超幾何級數的研究》是依託東北大學,由賈藏芝擔任項目負責人的青年科學基金項目。中文摘要 本項目旨在發展Abel方法及WZ算法的基礎上,開展橢圓超幾何級數的研究。橢圓超幾何級數是基本超幾何級數(q-級數)的推廣形式。它在計算數學、...
第2章 基本超幾何級數 10 2.1 從二項式定理到q-二項式恆等式 10 2.2 基本符號 13 2.3 基本超幾何級數 17 2.4 對*級數的Heine變換 20 2.5 Jackson*級數變換公式 27 2.6 q-Saalschütz求和公式 30 2.7 q-Gamma與q-Beta...
超幾何分布是統計學上一種離散機率分布。它描述了從有限N個物件(其中包含M個指定種類的物件)中抽出n個物件,成功抽出該指定種類的物件的次數(不放回)。稱為超幾何分布,是因為其形式與“超幾何函式”的級數展式的係數有關。超幾何...
藉助 Gauss 超幾何函式的二次變換公式,建立了參數為 1/4 的超幾何級數比值函式無窮乘積表達式及其不等式,揭示了符號差為 1/4 廣義模方程解的性質;(3)研究超幾何函式的 Landen 型不等式,二次變換公式及其推廣形式,單參數的廣義...
《基本超幾何恆等式和模等式的機器證明》是依託南開大學,由孫慧擔任項目負責人的青年科學基金項目。中文摘要 基本超幾何恆等式的證明是q級數領域研究的一個核心課題,其證明方法包括代數方法、數論方法、機器證明方法、運算元方法和組合方法等...
基本超幾何級數(q-級數)理論經過兩百年的發展,現在已經廣泛地套用到了數論、微分方程、組合數學、統計和物理等學科分支。近一個世紀伴隨著組合數學的發展,q-級數和組合數學之間的聯繫越來越密切。分拆理論這一門古老的學科也因為大大的...
組合反演技巧與WZ方法一樣是研究超幾何級數求和與變換的基本方法之一。本項目將主要研究申請人於2004年提出的(f,g)-反演在超幾何級數求和與變換方面的套用。我們將在初文昌研究工作的基礎上繼續深入探討並側重這一方法在特殊函式和正交...
楚德諾夫斯基算法是一種計算π的快速方法。簡介 楚德諾夫斯基算法是一種計算π的快速方法。楚德諾夫斯基兄弟使用它計算超過十億位數字。該算法基於以下快速收斂的超幾何級數:這個恆等式與拉馬努金的某些涉及 的公式非常相似。計算任意數位的方法 ...
pFq,超幾何級數。數學函式中表示非空集合A與B的2某種確定的對應關係,抽象概念化的f。物理學 °F表示華氏度。表示法拉第常數:F=96485.3383±0.0083C/mol。F,法拉(Farad),電容單位(國際單位制導出單位)。F,表示力(Force)...
數學中各學科的交叉研究是近年來的一個發展趨勢,本項目的研究重點是將組合方法與數論同餘和Rota-Baxter代數相結合,在以下幾個方面開展工作: (1)利用基本超幾何級數理論研究分拆同餘關係,本項目側重於S. Ramanujan在此類工作的研究...
泰勒發現的著名公式的研究中首創了後來成為處理高階方程主要手段的降階法;泰勒最先引起人們對奇異解存在性的注意;歐拉在1750年解出了一般的常係數線性方程,他還引進超幾何級數作為解二階線性方程的基礎;對全微分方程的研究亦由歐拉、...
1812年,高斯對一類具體的級數──超幾何級數,進行了嚴密研究,是歷史上第一項重要的有關級數收斂性的工作。1817年,波爾查諾首先拋棄無窮小量概念,用極限觀念給出導數和連續性的定義,並得到判別級數收斂的一般準則(現稱柯西準則),...
庫默爾在數論、幾何學、函式論、數學分析、方程論等方面都有較大的貢獻,但最主要的是在函式論、數論和幾何三個方面。在函式論方面。他研究了超幾何級數,首次對這些級數的單值群的代換進行計算。他發明的級數變換法是相當有名的,在...
(5)將Vandermonde卷積公式(5種)統一成一個超幾何級數恆等式及得到相關的超幾何級數變換,便於機械化證明。在恆等式機械化證明方面,克服吳方法在運算元代數中不可交換的困難。給出用吳方法證明恆等式的算法和軟體。在奔Ⅲ667機上這實現...
在哈代和李特爾伍德等人的幫助下,拉馬努金進步很快,在素數分布、堆壘數論、廣義超幾何級數、橢圓函式、發散級數等領域取得了很多成果.他在歐洲的5年裡發表了21篇論文,17篇註記,其中幾篇是與哈代合作的。他和哈代一起對整數分拆問題...
富克斯早期從事高等幾何和數論方面的研究,主要研究微分方程。他利用超幾何級數解線性微分方程;證明了定義在復域上的n階線性微分方程滿足給定初始條件的解的存在性;線性微分方程“基礎解系”的術語是由他引入的,討論這樣一個基礎解系的...
本項目研究多重zeta值的代數、幾何和算術性質。我們證明了Ohno-Zagier關係可以由正則化雙shuffle關係導出,從而同時給出了Ohno-Zagier關係的一個純代數證明。利用廣義超幾何級數3F2,我們給出了Zagier關於自變數為若干個2和一個3的多重zeta...
Ⅲ 超幾何級數講義 Ⅳ 數學註記 V 報告 第六部分 Riemann家書選輯 Riemann家書選輯 附錄 附錄I 俄譯本對本卷部分論文的注釋 附錄Ⅱ Riemann的超幾何級數講義及其意義 附錄Ⅲ Riemann對複變函數理論影響的檔案證據 附錄Ⅳ Bernhard ...
1.主持,國家自然科學基金面上項目(12271234):非交換、多變數混合型與橢圓型超幾何級數及其相關問題的研究;2.主持,國家自然科學基金面上項目(11871258):伴隨根系統的幾類超幾何級數與Mock Theta函式的研究;3.主持,國家自然科學基金面...
黎曼在常微分方程理論中自守函式的研究上也有建樹,在他的1858~1859年關於超幾何級數的講義和1867年發表的關於極小正曲面的一篇遺著中,他建立了為研究二階線性微分方程而引進的自守函式理論,即通稱的黎曼——許瓦茲定理。在偏微分方程...
我們利用一些數學工具和方法:選取適當收縮公式,利用發生函式與遞推關係,和角與差角的反正切公式,剩餘定理,使用微積分方法和複變函數方法,利用超幾何級數的求和公式及庫末(kummer)恆等式,二階矩陣A的n次冪A“中元素a11,a12,a21...
第三節 超幾何函式 一、 超幾何級數與超幾何函式 二、 超幾何函式的積分表達式 三、 鄰次函式和遞推關係式 四、 變換公式 五、 可用超幾何函式表示的初等函式 六、 超幾何函式的計算...
內容涉及丟番圖逼近、數的加性和積性理論、黎曼爹函式、不等式、積分、三角級數等分析的廣泛領域.1913年,哈代又發現了印度數學家拉馬努金(Ramanujan,S. A),他與拉馬努金在素數分布、加性數論、廣義超幾何級數、橢圓函式、發散級數等...
