基本介紹
- 中文名:拉格朗日公式
- 外文名:lagrange formula
- 涉及領域:信息科學、數學
- 發現者:約瑟夫·拉格朗日
- 發現者職業:法國數學家,物理學家
- 包括:拉格朗日方程等
拉格朗日
生平
科學成就
拉格朗日方程
簡介
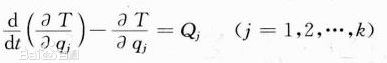
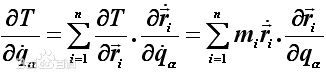
套用
插值公式
中值定理
定律定義






驗證推導












定理推廣
















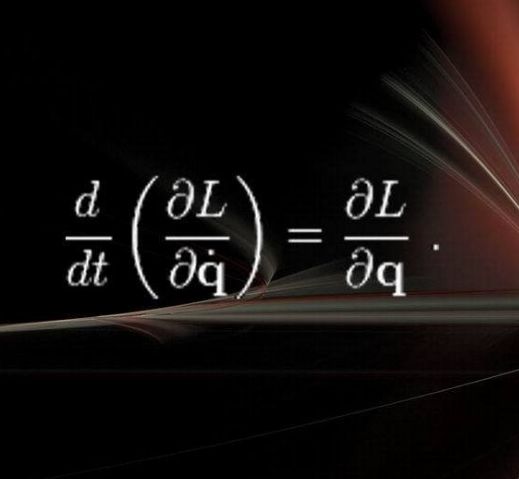
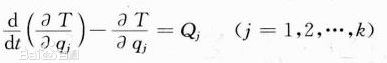
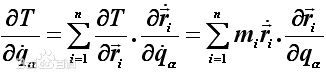


































上面第一式稱為拉格朗日中值公式,第二式和第三式稱為有限增量公式。拉格朗日中值定理也稱為有限增量定理,視其重要性,又稱為微分中值定理。推導驗證 設 ,由於 在閉區間 上連續,在 內可導,因此 在閉區間 上連續,在 內可導。又...
制約條件的公式表達式為:I=Px∙Qx+Py∙Qy。那么這一結論是如何推導出來的呢?解決這一問題最直接的方法就是拉格朗日乘數法。 上面說到:在利用偏導數求多元函式的極值時,若函式的自變數有附加條件,則稱之為條件極值。這時,可用拉格朗...
拉格朗日是一階偏微分方程理論的建立者,他在1772年完成的。“關於一階偏微分方程的積分”(Sur l'integration des équationau differences partielles du premier order)[21]和1785年完成的“一階線性偏微分方程的一般積分方法”(Méthode...
拉格朗日插值公式(外文名Lagrange interpolation formula)指的是在節點上給出節點基函式,然後做基函式的線性組合,組合係數為節點函式值的一種插值多項式。公式介紹 線性插值也叫兩點插值,已知函式y = f (x)在給定互異點x₀, x₁...
。對於任意 ,都有 使得 是n-1次多項式,且滿足 並且 。最後可得 。形如上式的插值多項式 稱為拉格朗日(Lagrange)插值多項式。例如:當n=4時,上面的公式可簡化為:這是一個過4個點的唯一的三次多項式。
。將這些公式代入拉格朗日方程,就可複製牛頓第二定律的方程:因此,這拉格朗日量被認定為正確無誤。這粒子的廣義動量 定義為 假設這物理系統的勢能為零,這粒子是自由粒子,則此系統的能量函式h為 這是質能方程:粒子的總能量等於其質量...
又稱平動點,在天體力學中是限制性三體問題的五個特解。一個小物體在兩個大物體的引力作用下在空間中的一點,在該點處,小物體相對於兩大物體基本保持靜止。這些點的存在由瑞士數學家歐拉於1767年推算出前三個,法國數學家拉格朗日於...
拉格朗日內插公式 最後要提一下他在《師範學校數學基礎教程》中,提出了著名的拉格朗日內插公式。直到現在計算機計算大量中點內插時仍在使用。另外在求多元函式相對極大極小及解微分方程中的拉格朗日任意乘子法,至今也在用。其他 除了對...
麥克勞林公式(Maclaurin's series)是泰勒公式的一種特殊形式。定義 麥克勞林公式是泰勒公式(在 ,記 )的一種特殊形式。在不需要餘項的精確表達式時,n階泰勒公式也可寫成 由此得近似公式 誤差估計式變為 在麥克勞林公式中,誤差|R𝗻...
張遂一牛頓插值公式(Zhang-Newton interpola-tion formula)亦稱牛頓插值公式一種便於計算的插值多項式,是拉格朗日插值公式的另一種表達形式.具體形式為 依次為零階均差,一階均差差(參見“均差”).,t階均差,n階均 ...
如果函式足夠光滑,在已知函式某一點各階導數的前提下,泰勒公式可以利用這些導數值作為係數構建一個多項式來近似該函式在這一點的鄰域中的值。1772年,拉格朗日強調了泰勒公式的重要性,稱其為微分學基本定理,但是泰勒定理的證明中並沒有...
插值型求積公式(interpolator quadrature for-mina)是一類最基本的求積公式.。為節點的n次拉格朗日插值多項式為 當全部求積節點xk任CQ,司時,稱為內插求積公式.由插值多項式(1)的性質,求積公式(2)的代數精確度至少是n.並且可以通過插值...
拉格朗日投影又稱“雙圓投影”。等角多圓錐投影中的一種。由法國數學家拉格朗日(1736~1813)於1779年提出,故名。赤道與中央經線均為直線並且正交,經線與緯線均為同軸圓的圓弧,其圓心位於中央經線與赤道的延長線上。概念 又稱“雙圓...
拉格朗日方程,因約瑟夫·路易斯·拉格朗日而命名,是拉格朗日力學的主要方程,可以用來描述物體的運動,特別適用於理論物理的研究。拉格朗日方程的功能相等於牛頓力學中的牛頓第二定律。簡介 拉格朗日方程:對於完整系統用廣義坐標表示的動力方程,...
拉格朗日公式 這是一個著名的公式,而且非常有用:(a×b)×c=b(a·c)-a(b·c)a×(b×c)=b(a·c)-c(a·b)證明過程如下:二重向量叉乘化簡公式及證明 可以簡單地記成“BAC-CAB”。這個公式在物理上簡化向量運算...
以下恆等式,稱作三重積展開或拉格朗日公式,對於任意向量 均成立:英文中有對於第一式有助記口訣BAC-CAB (BACK-CAB,後面的計程車),但是不容易記住第一式跟第二式的變化,很容易搞混。 觀察兩個公式,可得到以下三點:兩個分項...
阿貝公式中的放大率是 拉格朗日公式中放大率是 在一般情況下 M≠ M,也就是說從鏡頭邊緣折射的大角度光線和從鏡頭中心折射的小角度光線有不同的放大率。但是恩斯特·阿貝推論:如果鏡頭的球面像差和彗形像差得到完全得修正,這兩個...
(拉格朗日公式),特別地,(a×b)²=a²b²-(a·b)²。4.(a×b,b×c,c×a)= (a b c)²= .現在討論(a×b)c的幾何意義。在此假定a、b、c都是非零向量。將a、b、c移到共同始點,以它們為棱,作一個...
所得公式立即顯示插值多項式存在於上述定理中所述的條件下。 當對計算多項式的係數不感興趣時,在計算p(x)的值(給定的x不在原始數據集中)時,拉格朗日公式將優於范德蒙德公式。 在這種情況下,我們可以將複雜度降低到O(n²)。人...
稱為拉格朗日量,它依賴於φ,包括它在各點的導數和位置。換句話說,對於中的φ 設我們給出邊界條件,也即,在M為緊緻的情況下φ在邊界的取值,或者在x趨向∞時,φ的極限。則的由滿足如下兩個條件的的φ組成的子空間就是在殼解...
所得公式立即顯示插值多項式存在於上述定理中所述的條件下。 當對計算多項式的係數不感興趣時,在計算p(x)的值(給定的x不在原始數據集中)時,拉格朗日公式將優於范德蒙德公式。 在這種情況下,我們可以將複雜度降低到O(n²)。應...
