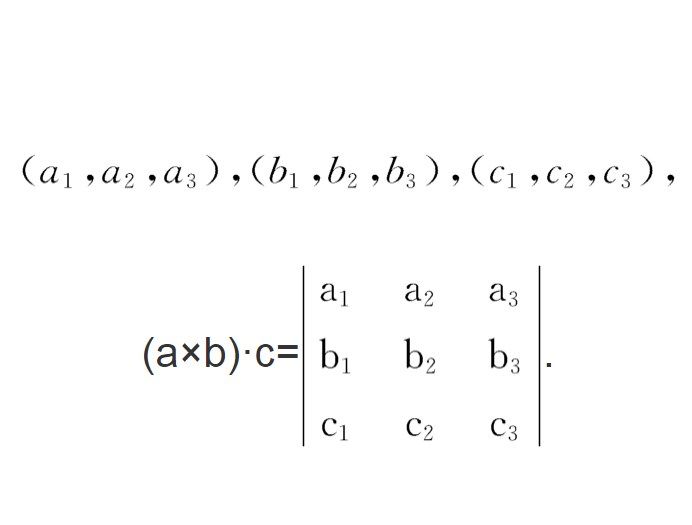數量三重積(scalar triple product)亦稱混合積,三個向量的一種乘法運算的結果。對於空間的三個向量a,b,c,數量(a×b)·c稱為向量a,b,c的數量三重積。幾何上,混合積的絕對值表示以a,b,c為棱的平行六面體的體積。若在平行六面體的同一頂點上的三條棱之間規定好一個順序(a,b,c),則稱這個平行六面體的定向為(a,b,c),於是混合積(a×b)·c稱為這個定向平行六面體的有向體積。(a×b)·c>0時成右手系,(a×b)·c<0時成左手系.(a×b)·c=0時,三個向量a,b,c共面。
基本介紹
- 中文名:數量三重積
- 外文名:scalar triple product
- 所屬問題:空間解析幾何
- 簡介:三個向量的一種乘法運算的結果
基本介紹,相關性質定理,
基本介紹
已知a、b、c三個向量,則a×b=d為一個向量,因此(a×b)·c=d·c是一個數量,於是有
定義 兩個向量先矢乘,再與另一向量數乘,所得的結果稱為數量三重積或者混合積。
相關性質定理
關於混合積有下列公式:
1.輪換混合積的三個因子,混合積的值不變;交換任何兩個因子,混合積變號。
2.(a×b)·c=a·(b×c)。因此a,b,c的混合積亦記為(abc)或(a,b,c)。
3.(a×b)·(c×d)=[(a×b)×c]·d= (拉格朗日公式),特別地,(a×b)=ab-(a·b)。
(拉格朗日公式),特別地,(a×b)=ab-(a·b)。

4.(a×b,b×c,c×a)= (a b c)= .
.

現在討論(a×b)c的幾何意義。在此假定a、b、c都是非零向量。
將a、b、c移到共同始點,以它們為棱,作一個平行六面體,並作d=a×b,設 是θ,底面積是S,高是h,體積是V,於是S={a×b|。在圖1(a)中,h=|c|cosθ,0<θ<π/2;在圖1(b)中,h=|c|cos(π-θ)=-|c|cos θ, π/2<θ<π;合併此兩式,得h=|c||cosθ|,又
是θ,底面積是S,高是h,體積是V,於是S={a×b|。在圖1(a)中,h=|c|cosθ,0<θ<π/2;在圖1(b)中,h=|c|cos(π-θ)=-|c|cos θ, π/2<θ<π;合併此兩式,得h=|c||cosθ|,又

V=hS=|a×b||c||cosθ|=|(a×b)c|
(由於體積總是正數,所以應取絕對值),由上式可以看出:(a×b)c是正或是負,取決於θ是銳角或是鈍角,也就是a×b和c是指向底面的同側或是異側,更明確地說, a、b、c形成右手系時,數量三重積是正;形成左手系時,則為負.故得
定理1 當三個非零向量a、b、c成右手系時,則數量三重積(a×b)c為正,否則為負。又此乘積的絕對值是以a、b、c為棱所構成的平行六面體的體積。
由於上述平行六面體也可以看作是以b、c或c、a作底面,故它的體積又可以寫作|(b×c)a|或|(c×a)b|,在此注意:a、b、c成右手系時,b、c、a或c、a、b也成右手系,故得
(a×b)c= (b×c)a=(c×a)b (1)
又因數量積適合交換律,故得
(a×b)c=c(a×b). (2)
由(1)及(2)得
(a×b)c= (b×c)a= (c×a)b=a(b×c)=b(c×a)=c(a×b). (3)
當a、b、c三者中有一個或兩個或三個是零向量時,則(3)中每個式子的值都是零.此六式通常以(a, b, c)來表示。
由數量三重積的定義及表示方法,可以得到以下各推論。
推論1 (a, a, c)=0. (4)
這是因為a×a=0。
推論2(a,b,c)=-(b,a, c). (5)
這是因為a×b=-(b×a).
推論3 (a+a', b, c)=(a,b,c)+(a', b, c). (6)
證明(a+a',b, c)=[(a+a')×b]c
=(a×b+a'×b)c
=(a×b)c+ (a'×b)c:
=(a, b, c)+(a', b, c).
推論4 (ma, b, c)=m(a, b, c). (7)
證明 (ma, b, c)= (maxb)c= [m(a×b)]c
=m[(a×b)c]=m(a, b, c).
利用三個向量的數量三重積可以研究三個向量是否共面的問題,這有下述定理:
定理2 三個向量中如果有一個為零,或者兩個共線,或者三個共面,則其數量三重積必是零,反過來也成立。
定理3 假定三個非零向量中沒有兩個共線,則共面的充要條件是其數量三重積為零。