基本介紹
- 中文名:三重積
- 外文名:triple product
- 定義:三個向量相乘的結果
- 分類:標量三重積和向量三重積
- 套用學科:數學
- 別稱:混合積
標量三重積
定義


特性






利用行列式的特性,可知順序置換向量的位置不影響標量三重積的值:

任意對換兩個向量的位置,標量三重積與原來相差一個負號:


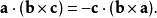
若任意兩個向量相等,則標量三重積等於零:

其他記號

幾何意義

向量三重積
定義



特性

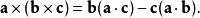

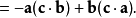
證明





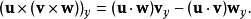

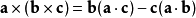



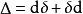












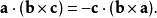







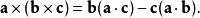

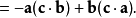





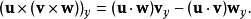

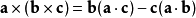



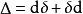
三重積,又稱混合積,是三個向量相乘的結果。向量空間中,有兩種方法將三個向量相乘,得到三重積,分別稱作標量三重積和向量三重積。...
若該和式當||T||→0時的極限存在且唯一(即與Ω的分割和點的選取無關),則稱該極限為函式f(x,y,z)在區域Ω上的三重積分,記為∫∫∫f(x,y,z)dV,...
數量三重積(scalar triple product)亦稱混合積,三個向量的一種乘法運算的結果。對於空間的三個向量a,b,c,數量(a×b)·c稱為向量a,b,c的數量三重積。幾何...
最主要的差別在於重積分的積分區域與定積分的積分區間相比更為複雜,函式的自變數也增多了,從而使得重積分理論與計算方法變得更豐富些,並且換元法是計算三重積分的一...
(注意同樣的體積也可以通過三變數常函式f(x,y,z) = 1在上述曲面和平面之間的區域中的三重積分得到。若有更多變數,則多維函式的多重積分給出超體積。...
廣義重積分(generalized multiple integral)是廣義黎曼重積分的簡稱,又稱反常重積分或非正常重積分,是一類多元函式積分,指無界多元函式及無界集上多元函式的積分 [1]...
三重積,又稱混合積,是三個向量相乘的結果。向量空間中,有兩種方法將三個向量相乘,得到三重積,分別稱作標量三重積和向量三重積。而向量三重積(vector triple ...
1.理解二重積分、三重積分的概念,了解重積分的性質,了解二重積分的中值定理.2.掌握二重積分的計算方法(直角坐標、極坐標),會計算三重積分(直角坐標、柱面坐標、...
一、三重積分的概念209二、三重積分的計算方法210?第五節曲線積分216一、對弧長的曲線積分216二、對坐標的曲線積分219三、格林公式223...
8.4三重積分的概念及計算方法8.4.1三重積分的概念8.4.2在直角坐標系中計算三重積分8.4.3在柱面坐標系中計算三重積分8.4.4在球面坐標系中計算三重積分...
4.1不定積分的概念與性質1124.1.1原函式與不定積分的概念1124.1.2基本積分表...*9.4三重積分3219.4.1三重積分的概念3219.4.2三重積分的計算方法3229.4...
不定積分、定積分及其套用、微分方程等內容,書末還附有二階和三階行列式簡介、...多元函式微分法及其套用、重積分、曲線積分與曲面積分、無窮級數等內容,書末還附...
第三節 多元函式的極值與最值第四節 多元函式微分學的幾何套用及方嚮導數與梯度第十章 重積分第一節 二重積分第二節 三重積分第三節 重積分的套用...
6.1.2定積分的概念 1186.1.3定積分的幾何意義 1196.1.4定積分的性質 120習題6.1 1226.2微積分基本公式 1226.2.1積分上限函式 123...
第九章 重積分82 第一節 二重積分82 習題9.190 第二節 三重積分91 習題9.2100 第三節 重積分的套用101 習題9.3109 綜合測試題(九)110 第十章 曲線積分與...
6.8多重積分6.8.1二重積分6.8.2三重積分第7章微分方程7.1常微分方程的數值解法7.1.1Euler方法7.1.2Runge-Kutta方法7.1.3Runge-Kutta方法解剛性問題7....
向量恆等式列表三重積 編輯 向量恆等式列表其他乘積 編輯 向量恆等式列表二次微分 編輯 這裡, 應被理解為對 的每個分量取拉普拉斯運算元,即向量值函式的拉普拉斯...
