多元函式的重積分理論與一元函式的定積分理論是平行的,最主要的差別在於重積分的積分區域與定積分的積分區間相比更為複雜,函式的自變數也增多了,從而使得重積分理論與計算方法變得更豐富些,並且換元法是計算三重積分的一種常用方法。
基本介紹
- 中文名:三重積分換元法
- 外文名:triple integral substitution
- 學科:數學
- 領域範圍:數學分析
- 屬性:重積分
重積分的定義










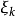





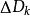



三重積分換元法
定理1






柱面坐標變換
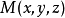
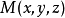


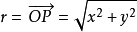


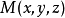



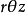






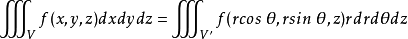




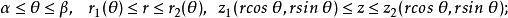
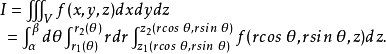
球面坐標變換
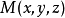













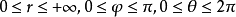
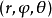








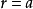






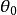




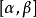





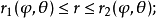



多元函式的重積分理論與一元函式的定積分理論是平行的,最主要的差別在於重積分的積分區域與定積分的積分區間相比更為複雜,函式的自變數也增多了,從而使得重積分理論與計算方法變得更豐富些,並且換元法是計算三重積分的一種常用方法。










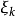





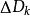









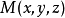
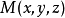


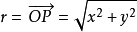


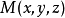



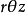






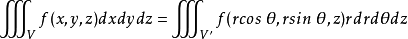




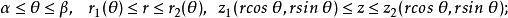
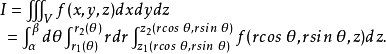
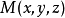













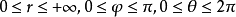
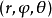








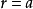






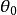




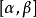





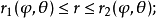



最主要的差別在於重積分的積分區域與定積分的積分區間相比更為複雜,函式的自變數也增多了,從而使得重積分理論與計算方法變得更豐富些,並且換元法是計算三重積分的一...
7.2.4 二重積分的換元法 習題7—2 7.3 三重積分的計算 7.3.1 直角坐標系下三重積分的計算 7.3.2 柱面坐標系與球面坐標系下三重積分的計算 習...
《理科類系列教材?微積分(第8版)(改編版)》在長期使用過程中,經不斷修訂,...14.6 利用柱面坐標和球面坐標計算三重積分14.7 二重積分的換元法;雅可比行列式...
三、二重積分的換元法 習題7-2(4)第三節 三重積分的計算一、利用直角坐標計算三重積分二、利用柱面坐標計算三重積分三、利用球面坐標計算三重積分 習題7-3...
計算二重積分(145) 習題7—2(2)(151) 三、二重積分的換元法(152)習題7—2(3)(156)第三節 三重積分的計算一、利用直角坐標計算三重積分(157) 二、利用...
9.6.1三重積分的換元法9.6.2利用柱面坐標計算三重積分9.6.2利用球面坐標計算三重積分習題9.6第10章曲線積分與曲面積分10.1對弧長的曲線積分(第一類曲線...
10.6.1三重積分的換元法10.6.2利用柱面坐標計算三重積分10.6.3利用球面坐標計算三重積分習題10.6第11章曲線積分與曲面積分11.1對弧長的曲線積分(第一類曲線...
10.3二重積分的換元法169 10.4二重積分的套用173 10.5三重積分的概念及其計算法175 10.6含參變數的積分179第11章曲線積分與曲面積分182 11.1曲線積分的定義...
四、二重積分換元法……… 134五、二重積分套用舉例……… 136習題7-1 ……… 142第二節 三重積分的概念、計算和套用……… 146一、三重積分的概念...
一元函式微分掌及其套用,一元函式積分學及其套用;下冊主要內容包括向量代數與空間...三、二重積分的換元法習題9.2第三節 三重積分一、三重積分的概念...
§10.2二重積分的計算法 10.2.1直角坐標系下二重積分的計算 10.2.2極坐標系下二重積分的計算 *10.2.3二重積分的換元法 §10.3三重積分 10.3.1三重積...
9.3.2 二重積分的換元法9.4 三重積分的概念及其計算9.4.1 三重積分的定義9.4.2 直角坐標系下三重積分的計算9.5 利用柱面和球面坐標計算三重積分...
習題16.1 二重積分的定義和基本性質習題16.2 直角坐標系下的二重積分的計算習題16.3 二重積分的換元法習題16.4 三重積分習題16.5 重積分...
三、二重積分的一般換元法習題9.2§9.3 三重積分的概念與計算一、三重積分的概念二、三重積分的計算習題9.3§9.4 重積分的套用...
