基本介紹
- 中文名:弗羅貝尼烏斯問題
- 外文名:Frobenius problem
- 所屬學科:數學
- 所屬問題:初等數論(不定方程)
- 簡介:關於一次不定方程的一個著名問題
- 別稱:換錢問題
基本介紹

相關證明













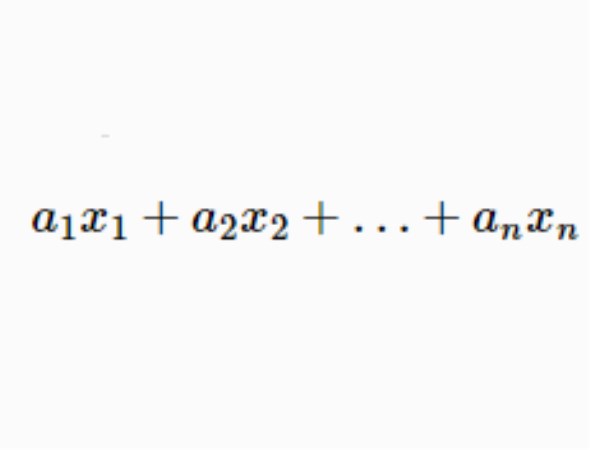














弗羅貝尼烏斯問題(Frobenius problem)是關於一次不定方程的一個著名問題。設a1,a2,…,an為整數,它們的最大公約數為1,求不能表示成a1x1+a2x2+…+anxn的最大...
群的抽象概念完成之後,弗羅貝尼烏斯開始研究抽象群理論中的具體問題.1887年,他證明了有限抽象群的敘洛夫(Sylow)定理,即如果一個有限群的階(有限群的階指它包含的...
所屬問題 高等代數(矩陣) 別稱 西爾維斯特不等式 簡介 矩陣乘積的秩與其因子...下面西爾維斯特(Sylvester)不等式也可由弗羅貝紐斯不等式的直接推得。故有的書籍...
數學 所屬問題 域論與伽羅瓦理論(域的擴張) 相關概念 有限域,分圓域等 目錄 1 基本介紹 2 相關概念 ▪ 有限域 ▪ 分圓函式域 弗羅...
於1959年在討論內射模的對偶性質時提出的,他提出了左PF環是否是右PF環的問題。狄斯勤格(Dischinger,F.)和繆勒(Mu¨ller,W.)於1986年證明了答案是否定的。
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯定理編輯 鎖定 討論 本詞條由“科普中國”科學百科詞條...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯方法編輯 鎖定 討論 本詞條由“科普中國”科學百科詞條...
套用範疇論時,關鍵是先搞清研究問題以什麼作對象,以什麼作態射(參見“範疇”).研究不同範疇之間的關係時,關鍵在於找到適當的函子。範疇論的核心是函子理論。艾倫...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 擬弗羅貝尼烏斯環編輯 鎖定 討論 本詞條由“科普中國”科學百科詞條...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯定理(第二形式)編輯 鎖定 討論 本詞條缺少信息欄、概述...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯準則編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯定理(經典形式)編輯 鎖定 討論 本詞條缺少信息欄、概述...
常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯代數編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關內容使詞條更完整,還...
這種理論有著廣泛的適用性,解決了一大批長期以來懸而未決的問題。另外,他在超複數系,微分方程的級數解、解析函式的冪級數和發散級數等方面也有建樹。福賽思(Forsyth...
合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯一佩龍定理編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關內容...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯互反律編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯同態編輯 鎖定 討論 本詞條缺少概述、信息欄、概述圖,...
常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯補編輯 鎖定 討論 本詞條缺少概述、信息欄、概述圖,補充相關內容使詞條更完...
常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯定理(第一形式)編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關內容使詞...
權威合作 合作模式 常見問題 聯繫方式個人中心 收藏 查看我的收藏 0 有用+1 已投票 0 弗羅貝尼烏斯映射編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關...
