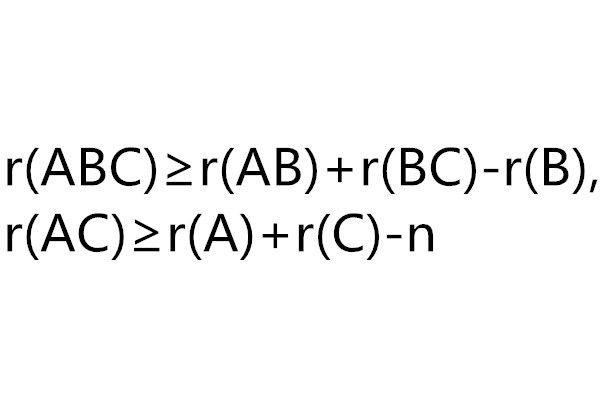弗羅貝尼烏斯不等式

弗羅貝尼烏斯不等式(Frobenius inequality)亦稱西爾維斯特不等式，是一種特殊不等式，指矩陣乘積的秩與其因子的秩之間的重要關係式。設矩陣A和B是可乘的，而B和C是可乘的，則r(ABC)≥r(AB)+r(BC)-r(B)，在此不等式中，若A為m×n矩陣，B為n階單位矩陣，C為n×s矩陣，則r(AC)≥r(A)+r(C)-n，有的書籍也稱第一種情況為弗羅貝尼烏斯不等式，第二種情況為西爾維斯特不等式。

基本介紹

• 中文名：弗羅貝尼烏斯不等式
• 外文名：Frobenius inequality
• 所屬學科：數學
• 所屬問題：高等代數(矩陣)
• 別名：西爾維斯特不等式
• 簡介：矩陣乘積的秩與其因子的秩的關係

基本介紹

設A、B、C分別為m×n，n×s，s×t矩陣，則：r(ABC)≥r(AB)+r(BC)－r(B)。

設，則r(AB)≥r(A)+r(B)－n。

弗羅貝尼烏斯不等式的證明

弗羅貝紐斯(Frobenius)不等式

設A、B、C分別為m×n，n×s，s×t矩陣，則：r(ABC)≥r(AB)+r(BC)－r(B)。

證明： 只要證明：

即可。

事實上，因為

所以

即

下面西爾維斯特(Sylvester)不等式也可由弗羅貝紐斯不等式的直接推得。故有的書籍也將其稱為弗羅貝紐斯不等式。

西爾維斯特(Sylvester)不等式

設，則r(AB)≥r(A)+r(B)－n。

證明 只要證明：

事實上，由

知

證完。