基本介紹
- 中文名:局部有界空間
- 外文名:locallybondedspace
- 所屬領域:數理科學
- 屬性:一類拓撲線性空間
- 提出者:亥爾斯(D.H.Hyers)
- 引入時間:1939年
基礎概念
定義



相關概念





















相關性質定理
命題1




定理1





推論






命題2

命題3
命題4



定理2














定理3











推論1
推論2



定理4


定理5













































































局部有界空間是一類拓撲線性空間,如果拓撲線性空間E中存在零元的一個有界的鄰域,則稱E是局部有界的。局部有界空間是亥爾斯(D.H.Hyers)於1939年引入的,局部有界空間也一定是度量線性空間。基礎概念定義設 是拓撲線性...
3.4局部p-凸空間中的Hahn―Banach定理 3.5評註與參考資料 第4章局部有界空間 4.1有界集合 4.2局部有界空間 4.2.1集合凹性模 4.2.2空間凹性模 4.2.3局部有界空間的可賦p-范性 4.3局部有界萬有空間 4.3.1賦...
X為局部有界空間,若且唯若𝔅中存在有界集。同時為T1空間的X是完全正則空間。同時為T₁空間的X是豪斯多夫空間。若Z是X的子空間,則Z的閉包亦然。若Z是X的凸集,則Z的閉包亦然。若Z是X的均衡集,則Z的閉包亦然。若Z是X的...
有界型空間 有界型空間(bornologic space)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
以Gauss測度空間為例建立了相應的奇異積分運算元的有界性等;建立了加局部權的非齊型Triebel-Lizorkin空間的一些特徵刻畫, 原子分解, 以及局部奇異積分運算元在這些函式空間上的有界性等. 在齊型空間上, 系統地建立了齊型空間上的多線性運算元...
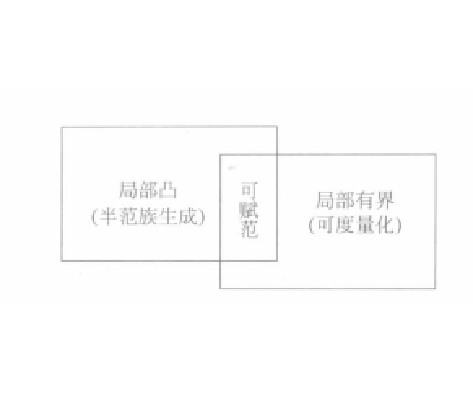
設E是拓撲線性空間,如果E上還存在一個範數||·||,使||·||導出的拓撲與E中原來的拓撲相同,則稱E是可賦范的。判定 拓撲線性空間可賦范的充分必要條件是滿足下面三條:1.E滿足T₀公理;2.E是局部凸的;3.E是局部有界的。
即每一個第二可數的正規Hausdorff空間可度量化(通常會在點集拓撲的課程中介紹),另一個則是Bing-Nagata-Smirnov度量化定理,即一個拓撲空間可度量化若且唯若它是正則Hausdorff空間並且具有一個可數的局部有限基。
類似地,我們可以定義局部有界鞅、局部平方可積鞅等概念。由定義我們可以看出以下事實:1)局部鞅為一右連左極適應過程;2)右連續鞅為局部鞅(令 );3)局部鞅空間為線性空間;4)設M為局部鞅,T為停時,則 為局部鞅。基本性質 性質1...
F空間又簡稱Fréchet空間(Fréchet space)。為了和Banach空間那一條中的Fréchet空間有所區別,有時稱後者為Banach意義下的Fréchet空間(Fréchet space in the sense of Banach)。F空間是有界型的並且是桶型的。兩個局部凸空間之間的連續...
連續,根據連續函式的局部有界性可知存在 ,使得在 內有界。取上述的 ,則存在 ,當 時,,從而 在閉域 上有界,這與條件(iii)矛盾。所以 在閉域 上有界。證畢。上述用閉域套定理對有界閉域上二元連續函式的有界性定理進行證明...
有界且邊界 是 (此處指在局部邊界可以表示為一個 函式的圖像),選擇任何一個有界開集 滿足 (此處指存在一個緊集 滿足 )。則存在一個有界線性運算元 滿足對於任何 有 (i) 在 中幾乎處處:;(ii)的支集包含於 ;(iii...
線上性空間的對偶概念基礎上所形成的對偶理論是局部凸空間理論的中心內容,它也是把局部凸空間和它的共軛空間放在相對稱的地位來加以研究的。可允許拓撲 可允許拓撲是一種局部凸拓撲。設(X,Y)是對偶線性空間,Y是Y中的有界集族,且...
設E是局部凸空間,則賦予強拓撲的共扼空間E'的共扼空間E''包含原來的空間E,當E" = E時,稱E是半自反的。進一步當E的拓撲和強拓撲β(E,E')一致時,稱E為自反的。E為半自反的充分必要條件是E的任意有界弱閉凸集是弱緊的。...
桶型空間(barreled space)是一類局部凸空間。設E是局部凸空間,E中的吸收的均衡凸閉集稱為桶集。在序列完備空間中,因而在有界完備空間中,桶集吸收每個有界集。如果局部凸空間E的每個桶集都是零元的鄰域,則E稱為桶型空間。E成為桶...
但在比Banach空間更廣泛的一類重要的拓撲線性空間-局部凸空間中,卻很少發現一般的變分原理。本項目通過引入一種次線性拓撲-Minkowski拓撲,進而討論這種拓撲空間中凸函式的微分性質,並套用這些微分性質以及罰函式的方法研究局部凸空間有界集上...
有界列是一種特殊的序列。對於數列{xₙ},若存在實數M(m),使對所有n∈N,有xₙ≤M(xₙ≥m),則稱{xₙ}有上(下)界。既有上界又有下界的數列稱為有界數列,簡稱有界列。簡介 有界列是一種特殊的序列。對於數列{x...
除此之外,我們還研究了張量積空間的相關幾何性質以及在有界集上弱連續的連續n-齊次多項式構成的空間的弱序列完備性,討論了賦范平面上Cassini曲線的幾何性質及其與空間幾何性質之間的關係。與此同時,我們還研究了賦范線性空間中的完備集,...
本項目主要目標:研究(1)有界度量空間能夠嵌入到自反、超自反、一致凸和HILBERT空間的特徵;(2)一般可分度量空間嵌入到一致凸空間和HILBERT空間的特徵;(3)球覆蓋行為在超自反和Hilbert空間的行為;(4)尋求有界幾何嵌入到一致凸空間...
本項目利用非可加測度的自連續性、零可加性、雙零可加性以及雙零漸近可加性等性質討論了關於單調非可加測度的可測實值函式空間的基本拓撲性質,得到了此空間滿足完備性、可分性、局部有界性、局部凸性的充分條件,及空間的偽度量化且...
本書講述拓撲線性空間的一般理論和它們的某些套用。全書由六章和兩個附錄組成。前面三章敘述拓撲線性空間的基本理論。作品目錄 前 言 第一章 拓撲線性空間 1. 1 線性空間 1. 2 拓撲線性空間的局部基 1. 3 有界性 可度量化 完備...
顯然,T在x₀處連續→T在x₀處半連續且T在x₀處局部有界。命題1.2,設T是極大單調運算元,[xₙ,yₙ]∈G(T)滿足xₙ→x,yₙ→y且 ,則[x,y]∈G(T) 且 。命題1.3,設T:X→X'是半連續單調運算元,且D(T...
可允許拓撲是一種局部凸拓撲,也可稱為集類𝒴上的一致收斂拓撲,而相應的有界集族𝒴稱為可允許集族。簡介 可允許拓撲是一種局部凸拓撲。設(X,Y)是對偶線性空間,𝒴是Y中的有界集族,且並U{A|A∈𝒴}的線性...
強拓撲(strong topology)是一種拓撲。局部凸空間X中原有的拓撲,相對於弱拓撲σ(X,X)稱為X的強拓撲。例如賦范線性空間的強拓撲即為範數拓撲。對於共軛空間X,記B為X中有界子集全體,對每個有界子集B∈B,定義半範數:則由半範數族...
若且唯若處處可微函式f的一次導函式有界,f符合利普希茨條件。這是中值定理的結果。所有 函式都是局部利普希茨的,因為局部緊緻空間的連續函式必定有界。性質 符合利普希茨條件的函式一致連續,也連續。bi-Lipschitz函式是單射的。Rademach...
