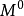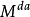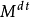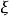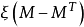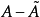基本介紹
- 中文名:局部鞅
- 外文名:local martingale
- 簡稱:局鞅
- 所屬學科:數學
- 性質:鞅的局部化類
定義,基本性質,基本定理與局鞅分解,
定義
設M為一右連續適應過程,稱M為一局部鞅(相應地,局部上鞅,局部可積變差鞅),如果存在停時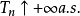 ,使得每個
,使得每個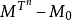 為一致可積鞅(相應地,類(D)上鞅,可積變差鞅).
為一致可積鞅(相應地,類(D)上鞅,可積變差鞅).
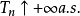
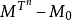
類似地,我們可以定義局部有界鞅、局部平方可積鞅等概念。
由定義我們可以看出以下事實:
1)局部鞅為一右連左極適應過程;
2)右連續鞅為局部鞅(令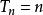 );
);
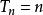
3)局部鞅空間為線性空間;
4)設M為局部鞅,T為停時,則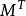 為局部鞅。
為局部鞅。
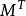
基本性質
性質1 設M為一非負局部上鞅,若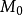 可積,則M為上鞅。
可積,則M為上鞅。
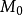
性質2 設M為一右連續適應過程,
1)為要M是局部鞅,必須且只需存在停時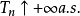 ,使得每個
,使得每個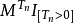 為一致可積鞅。
為一致可積鞅。
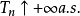
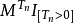
2)設S,T為兩個停時,使得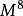 及
及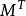 為一致可積鞅,則
為一致可積鞅,則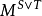 也為一致可積鞅。
也為一致可積鞅。
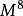
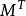
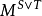
3)如果存在停時列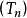 ,使得
,使得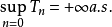 ,且每個
,且每個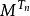 為局部鞅,則M為局部鞅。
為局部鞅,則M為局部鞅。
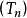
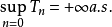
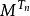
性質3 設M為一局部鞅,T為一停時,則為要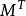 為一致可積鞅,必須且只需
為一致可積鞅,必須且只需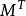 為類(D)過程。
為類(D)過程。
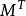
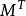
性質5 可料局部鞅為連續局部鞅。
性質6 設M為一可料的局部可積變差鞅,則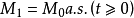 。
。
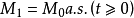
性質8 設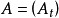 為一適應局部可積變差過程,
為一適應局部可積變差過程,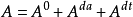 ,其中
,其中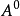 為A的連續部分,
為A的連續部分,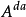 為A的可及跳部分,
為A的可及跳部分,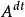 為A的絕不可及跳部分,則
為A的絕不可及跳部分,則
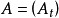
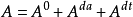
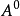
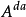
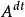
1)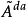 為純斷的,
為純斷的,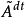 為連續的;
為連續的;
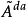
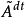
2)為要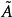 連續,必須且只需
連續,必須且只需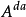 為局部鞅;
為局部鞅;
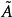
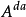
3)為要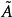 純斷。必須且只需
純斷。必須且只需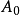 =0,且
=0,且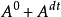 為局部鞅。
為局部鞅。
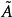
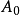
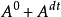
性質9 設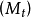 為一局部可積變差鞅,令
為一局部可積變差鞅,令
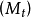
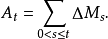
則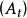 為一局部可積變差過程,且其可料對偶投影
為一局部可積變差過程,且其可料對偶投影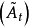 連續.我們有
連續.我們有
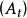
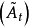
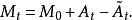
此外,若M只有可及跳,則
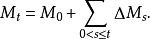
性質10 設X為一非負右連續上鞅,則X有如下唯一分解:
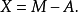
其中M為在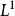 中有界的局部鞅,A為一零初值可料可積增過程。
中有界的局部鞅,A為一零初值可料可積增過程。
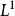
基本定理與局鞅分解
1.設M為一局部鞅,則對任給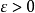 ,M可作如下分解:
,M可作如下分解:
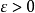
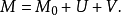
其中U為零初值局部有界鞅,且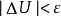 ;V為局部可積變差鞅,如果M擬左連續,則可要求U及V也擬左連續,且U與V無公共跳。
;V為局部可積變差鞅,如果M擬左連續,則可要求U及V也擬左連續,且U與V無公共跳。
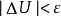
2. 有限變差局部鞅為局部可積變差鞅。
3. 設A為一適應有限變差過程,則為要A為局部可積變差過程,必須且只需存在一可料有限變差過程B使得A 一B為局部鞅。
4. 設M為一局部鞅,稱M為純斷局部鞅,如果世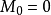 ,且M可作如下分解:
,且M可作如下分解:
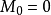
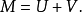
其中U為零初值局部純斷平方可積鞅,V為零初值有限變差局部鞅。
5. 設M為一局部鞅,則M有如下唯一分解:
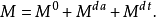
其中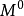 為連續局部鞅,
為連續局部鞅,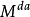 為只有可及跳的純斷局部鞅,
為只有可及跳的純斷局部鞅,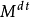 為只有絕不可及跳的純斷局部鞅。
為只有絕不可及跳的純斷局部鞅。