人物簡介,人物生平,1811及1812年,1813年,1815-1821,1830後,個人軼事,綽號,出名,晚年,巴黎紙貴,個人成就,單複變函數,分析基礎,極限論的功能,常微分方程,彈性力學數學理論,其他,
人物簡介 柯西(Cauchy, 1789—1857)是法國
數學家 、
物理學家 、
天文學家 。19世紀初期,
微積分 已發展成一個龐大的分支,,內容豐富,套用非常廣泛。與此同時,它的薄弱之處也越來越暴露出來,微積分的理論基礎並不嚴格。為解決新問題並澄清微積分概念,數學家們展開了
數學分析 嚴謹化的工作,在分析基礎的奠基工作中,做出卓越貢獻的要首推偉大的數學家柯西。
柯西畫像 柯西1789年8月21日出生於
巴黎 。父親是一位精通古典文學的律師,與當時法國的大數學家
拉格朗日 與
拉普拉斯 交往密切。柯西少年時代的數學才華頗受這兩位數學家的讚賞,並預言柯西日後必成大器。拉格朗日向其父建議“趕快給柯西一種堅實的文學教育”,以便他的愛好不致把他引入歧途。父親因此加強了對柯西的文學教養,使他在詩歌方面也表現出很高的才華。
1807年至1810年柯西在工學院學習,曾當過交通道路工程師。由於身體欠佳,接受了拉格朗日和拉普拉斯的勸告,放棄工程師而致力於純數學的研究。柯西在數學上的最大貢獻是在微積分中引進了極限概念,並以極限為基礎建立了邏輯清晰的分析體系。這是微積分發展史上的精華,也是柯西對人類科學發展所做的巨大貢獻。
1821年柯西提出極限定義的方法,把極限過程用不等式來刻畫,後經魏爾斯特拉斯改進,成為現在所說的柯西極限定義或叫
定義。當今所有微積分的教科書都還(至少是在本質上)沿用著柯西等人關於極限、連續、導數、收斂等概念的定義。他對微積分的解釋被後人普遍採用。柯西對定積分作了最系統的開創性工作,他把定積分定義為和的“極限”。在定積分運算之前,
強調 必須確立積分的存在性。他利用中值定理首先嚴格證明了
微積分基本定理 。通過柯西以及後來魏爾斯特拉斯的艱苦工作,使數學分析的基本概念得到嚴格的論述。從而結束微積分二百年來思想上的混亂局面,把微積分及其推廣從對幾何概念、運動和直觀了解的完全依賴中解放出來,並使微積分發展成現代數學最基礎最龐大的數學學科。
數學分析嚴謹化的工作一開始就產生了很大的影響。在一次學術會議上柯西提出了級數收斂性理論。會後,拉普拉斯急忙趕回家中,根據柯西的嚴謹判別法,逐一檢查其巨著《天體力學》中所用到的級數是否都收斂。
柯西在其它方面的研究成果也很豐富。
複變函數 的微積分理論就是由他創立的。在
代數 方面、
理論物理 、光學、
彈性理論 方面,也有突出貢獻。柯西的數學成就不僅輝煌,而且數量驚人。柯西全集有27卷,其論著有800多篇,在數學史上是僅次於歐拉的多產數學家。他的光輝名字與許多定理、準則一起銘記在當今許多教材中。
作為一位學者,他思路敏捷,功績卓著。從柯西卷帙浩大的論著和成果,人們不難想像他一生是怎樣孜孜不倦地勤奮工作。但柯西卻是個具有複雜性格的人。他是忠誠的保王黨人,熱心的天主教徒,落落寡合的學者。尤其作為久負盛名的科學泰斗,他常常
忽視 青年學者的創造。例如,由於柯西“失落”了才華出眾的年輕數學家
阿貝爾 與
伽羅華 的開創性的論文手稿,造成
群論 晚問世約半個世紀。
1857年5月23日柯西在巴黎病逝。他臨終的一句名言“人總是要死的,但是,他們的業績永存。”長久地叩擊著一代又一代學子的心扉。
德國數學家魏爾斯特拉斯 柯西在純數學和
套用數學 的功力是相當深厚的,在
數學 寫作上,他是被認為在數量上僅次於
歐拉 的人,他一生一共著作了789篇論文和幾本書,其中有些還是經典之作,不過並不是他所有的創作質量都很高,因此他還曾被人批評高產而輕率,這點倒是與數學王子相反,據說,
法國 科學院''會刊''創刊的時候,由於柯西的作品實在太多,以致於科學院要負擔很大的印刷費用,超出科學院的預算,因此,科學院後來規定論文最長的只能有四頁,所以,柯西較長的論文只得投稿到其它地方。
歐拉 柯西在幼年時,他的父親常帶領他到法國參議院內的辦公室,並且在那裡指導他進行學習,因此他有機會遇到參議員
拉普拉斯 和
拉格朗日 兩位大數學家。他們對他的才能十分賞識;拉格朗日認為他將來必定會成為大數學家,但建議他的父親在他學好文科前不要學數學。
人物生平 1811及1812年 柯西於1802年入中學。在中學時,他的拉丁文和希臘文取得優異成績,多次參加競賽獲獎;數學成績也深受老師讚揚。他於1805年考入綜合工科學校,在那裡主要學習數學和力學;1807年考入橋樑公路學校,1810年以優異成績畢業,前往
瑟堡 參加海港建設工程。
柯西 柯西去瑟堡時攜帶了拉格朗日的《
解析函式 論》和拉普拉斯的《
天體力學 》,後來還陸續收到從
巴黎 寄出或從當地借得的一些數學書。他在業餘時間悉心攻讀有關數學各分支方面的書籍,從
數論 直到天文學方面。根據拉格朗日的建議,他
進行 了多面體的研究,並於1811及1812年向科學院提交了兩篇論文,其中主要成果是:
(1)證明了凸正多面體只有五種(面數分別是4,6,8,12,20),星形正多面體只有四種(面數是12的三種,面數是20的一種)。
(2)得到了歐拉關於多面體的頂點、面和棱的個數關係式的另一證明並加以推廣。
(3)證明了各面固定的多面體必然是固定的,從此可導出從未證明過的
歐幾里得 的一個定理。
這兩篇論文在數學界造成了極大的影響。柯西在瑟堡由於工作勞累生病,於1812年回到巴黎他的父母家中休養。
1813年 柯西於1813年在巴黎被任命為運河工程的工程師,他在巴黎休養和擔任工程師期間,繼續潛心研究數學並且參加學術活動。這一時期他的主要貢獻是:
費馬 (1)研究代換理論,發表了代換理論和
群論 在歷史上的基本論文。
(2)證明了
費馬 關於多角形數的猜測,即任何正整數是個角形數的和。這一猜測當時已提出了一百多年,經過許多數學家研究,都沒有能夠解決。以上兩項研究是柯西在瑟堡時開始進行的。
(4)研究液體表面波的傳播問題,得到
流體力學 中的一些經典結果,於1815年得法國科學院數學大獎。
以上突出成果的發表給柯西帶來了很高的聲譽,他成為當時一位國際上著名的青年數學家。
1815-1821 1815年法國
拿破崙 失敗,波旁王朝復辟,
路易十八 當上了法王。柯西於1816年先後被任命為法國科學院院士和綜合工科學校教授。1821年又被任命為
巴黎大學 力學教授,還曾在
法蘭西學院 授課。這一時期他的主要貢獻是:
拿破崙 (1)在綜合工科學校講授分析課程,建立了微積分的基礎
極限理論 ,還闡明了極限理論。在此以前,微積分和
級數 的概念是模糊不清的。由於柯西的講法與傳統方式不同,當時學校師生對他提出了許多非議。
柯西在這一時期出版的著作有《代數分析教程》、《無窮小分析教程概要》和《微積分在幾何中套用教程》。這些工作為微積分奠定了基礎,促進了數學的發展,成為數學教程的典範。
(2)柯西在擔任巴黎大學力學教授後,重新研究
連續介質力學 。在1822年的一篇論文中,他建立了彈性理論的基礎。
(3)繼續研究複平面上的積分及留數計算,並套用有關結果研究數學物理中的偏微分方程等。
他的大量論文分別在法國科學院論文集和他自己編寫的期刊“數學習題”上發表。
1830後 1830年法國爆發了推翻波旁王朝的革命,法王
查理 第十倉皇逃走,
奧爾良公爵 路易·菲力浦繼任法王。當時規定在法國擔任公職必須宣誓對新法
王效忠 ,由於柯西屬於擁護波旁王朝的正統派,他拒絕宣誓效忠,並自行離開法國。他先到瑞士,後於1832~1833年任義大利
都靈 大學數學物理教授,並參加當地科學院的學術活動。那時他研究了複變函數的級數展開和
微分方程 (強級數法),並為此作出重要貢獻。
巴黎爆發了反對波旁王朝的革命 1833~1838年柯西先在
布拉格 、後在戈爾茲擔任波旁王朝“王儲”
波爾多 公爵的教師,最後被授予“男爵”封號。在此期間,他的研究工作進行得較少。
1838年柯西回到巴黎。由於他沒有宣誓對法王效忠,只能參加科學院的學術活動,不能擔任教學工作。他在創辦不久的法國科學院報告“和他自己編寫的期刊分析及數學物理習題”上發表了關於複變函數、天體力學、
彈性力學 等方面的大批重要論文。
1848年法國又爆發了革命,路易·菲力浦倒台,重新建立了共和國,廢除了公職人員對法王效忠的宣誓。柯西於1848年擔任了巴黎大學數理天文學教授,重新進行他在法國高等學校中斷了18年的教學工作。
路易十四一家 1852年拿破崙第三發動政變,法國從共和國變成了帝國,恢復了公職人員對新政權的效忠宣誓,柯西立即向巴黎大學辭職。後來拿破崙第三特準免除他和物理學家阿拉果的忠誠宣誓。於是柯西得以繼續進行所擔任的教學工作,直到1857年他在巴黎近郊逝世時為止。柯西直到逝世前仍不斷參加學術活動,不斷發表科學論文。
1857年5月23日,他突然去世,享年68歲,他因為熱病去世,臨終前,他還與巴黎大主教在說話,他說的最後一句話是:
“人總是要死的,但是,他們的功績永存。”
個人軼事 綽號 柯西在學生時代,有個綽號叫『苦瓜』,因為他平常像一顆苦瓜一樣,靜靜地不說話,如果說了什麼,也很簡短,令人摸不著頭緒,和這種人溝通,是很痛苦的。柯西的身邊沒有朋友,只有一群妒嫉他聰明的人。當時法國正在流行社會哲學,柯西工作之餘常看的書,卻是拉格朗日(Joseph Louis Lagrance,1736-1813)的數學書,與靈修書籍《效法基督》,這使他贏得另一個外號『腦筋劈哩啪啦叫的人』,意即神經病。
柯西 柯西的母親聽到了傳言,就寫信問他實情。柯西回信道:『如果基督徒會變成精神病人,那瘋人院早就被哲學家充滿了。親愛的母親,您的孩子像原野上的風車,數學和信仰就是他的雙翼一樣,當風吹來的時候,風車就會平衡地旋轉,產生幫助別人的動力。』
1816年,柯西回到巴黎,擔任母校的數學教授,柯西自己寫道:『我像是找到自己河道的鮭魚一般地興奮。』不久他就結婚,幸福的婚姻生活,有助於他與別人溝通的能力。
出名 數學大師
伯努利 曾說過:『只有數學能夠探討「無窮」,而「無窮」正是上帝的屬性之一』。物理、化學、生物都是有限之內的學科,『無窮』才能代表永遠測不透的極限。『無窮』的觀念令哲學家瘋征、讓神學家嘆息,使許多人深感懼怕。柯西卻把『無窮』套用來厘定更精確的數學含義,他把數學的微分看或是『無窮小時的變化』,把積分表示為『無窮多個無窮小之和』。柯西用無窮重新定義微積分,至今仍為每一本微積分課本的開宗明義篇。
柯西任教的巴黎大學 1821年,柯西的名聲遠播。遠自柏林、馬德里、聖彼得堡的學生,都來到他的教室里上課,他又發表非常有名的『特徵值』理論,同時寫道:『在純數學的領域裡,似乎沒有實際的物理現象來印證,也沒有自然界的事物可說明,但那是數學家遙遙望見的應許之地。理論數學家不是一個發現者,而是這個應許之地的報導者』。
晚年 四十歲後的柯西不願對新政府效忠,他認為學術應有不受政治影響的自由。他放棄工作與祖國,帶著妻子到瑞士、義大利旅行教書,各地大學都很歡迎他。但是他寫道:『對數學的興奮,是身體無法長期的負荷,累!』柯西四十歲後,下課後就不再做研究工作了。
他身體逐漸衰弱,一八三八年他再回巴黎大學教書,但為政治效忠問題再度離開。因著他的堅持,一八四八年法國通過大學教授的學術自由,是以個人的良心為底限,不在政治限制之內。從此世界各大學紛紛跟進這個制度,大學成為學術自由的地方。
巴黎紙貴 傳說柯西年輕的時候向巴黎科學院學報投論文,非常之快,非常之多使得印刷廠為了印製這些論文搶購了巴黎市所有紙店的存貨,使得市面上紙張短缺,紙價大增,印刷廠成本上升,於是科學院通過決議,以後發表論文每篇篇幅不得超過4頁。柯西不少長篇論文不得在本國發表,只能改投別國刊物。
個人成就 柯西是一位著名的多產數學家,他的全集從1882年開始出版到1974年才出齊最後一卷,總計28卷。他的主要貢獻如下;
單複變函數 柯西最重要和最有首創性的工作是關於單複變函數論的。18世紀的數學家們採用過上、下限是
虛數 的定積分。但沒有給出明確的定義。柯西首先闡明了有關概念,並且用這種積分來研究多種多樣的問題,如實定積分的計算,級數與無窮乘積的展開,用含參變數的積分表示微分方程的解等等。
分析基礎 柯西在綜合工科學校所授分析課程及有關教材給數學界造成了極大的影響。自從
牛頓 和
萊布尼茨 發明微積分(即無窮小分析,簡稱分析)以來,這門學科的理論基礎是模糊的。為了進一步發展,必須建立嚴格的理論。柯西為此首先成功地建立了
極限論 。
極限論的功能 設
函式 f(x)在點x。的某一
去心鄰域 內有定義,如果存在常數A,對於任意給定的正數ε(無論它多么小),總存在正數δ,使得當x滿足不等式0<|x-x。|<δ時,對應的函式值f(x)都滿足不等式:
|f(x)-A|<ε
那么常數A就叫做函式f(x)當x→x。時的極限。
“嚴格來說,沒有
數學證明 這種東西,分析到最後,除了指指點點,我們什麼也不會幹;……證明就是我和李托
伍德 叫做神吹的那套玩意兒,是編出來打動人心的花言巧語,是上課夠在黑板上的圖畫,是激發學生想像力的手法。”——哈代。
數學太重要了,在
中國 與語文學有著同樣的地位。其原因就在於數學本身就是一種語言,而且是一種世界語言,具有普遍性。所以,嚴格的區分數學概念的詞性,是非常有必要的,不僅是數學本身的要求,也是語言科學的要求。
談到語言和詞性,就要了解部分語文基礎知識了。
1、名詞:表示人或事物、處所、方位等名稱 的詞。
2、動詞:表示動作行為、發展變化、心理活動等意義的詞。
微積分從誕生的第一天開始,就沒有離開過矛盾和駁論。例如,
貝克萊 駁論(無窮小駁論)、芝諾悖論等。如果,透過這些爭論,可以發現其實他們不過是變相的探討最終形態的問題!正如
萊布尼茲 關注微粒最終命運一樣。有一些人說:柯西-威爾斯特拉斯的極限定義
, 有“極限迴避”的現象。這種說法是片面的也是不客觀的,但還是指出了一些問題(應該說最終形態迴避)。柯西-威爾斯特拉斯的極限定義,被翻譯成
中國語言 的時候,是非常經典的。柯西-威爾斯特拉斯的極限定義,不單純的定義了極限,還刻畫了一種運動現象-向極限(最終形態)靠近的運動。最後畫龍點睛,把最終形態a(如果存在,就是說不清怎么來的)叫做極限。
從語法的分析上看,這個說法本質上給了“最終形態”一個稱謂(名字)--極限。所以,柯西-威爾斯特拉斯的極限定義中,極限是一個名詞,而不是動詞。
於是,就把向極限靠近的運動叫做極限現象。許多人在理解柯西-威爾斯特拉斯的極限定義,混淆了極限現象與極限,籠統的把“極限現象”和“極限”都叫做極限。
關於最終形態的研究,我曾在《微積分秘密報告4》中簡單的談過。既然現代函式極限定義並沒有解釋最終形態(迴避了)!那么,函式的極限定義是要說些什麼故事呢?有關的數學證明又在證明什麼呢?
其實,是在說一件事:有極限(最終形態),必有極限現象;反過來,有極限現象,必有極限存在!簡單來說,就是極限現象是極限(最終形態)的充要條件。所以,要證明極限存在(不必去研究怎么來的),只需證明極限現象存在就夠了,確實有投機取巧的嫌疑!
就因為如此,所以現代極限的定義不能告訴你極限怎么來的,只能告訴你極限存在(並且可以證明)。極限現象就本質來看是一種運動現象,描述運動現象的理想工具是什麼-函式。所以現代的函式(專業)極限定義,有些函式的味道(一一對應,總有ε和δ對應)也就不起怪了。
有一些人也挺離譜的,把極限說成是動詞。理由是,極限的本質是:“一個變化的量無限接近一個固定的量。”這是極限現象的精髓,不是極限的。
可是,要描述極限現象。非要柯西-威爾斯特拉斯繞口的模型嗎!當然不是,模型是可以改變的,微積分初等化,就改變了這一模型。使一些複雜的數學證明得到了簡化,比如極限的唯一性、函式單調性等。
在柯西的著作中,沒有通行的語言,他的說法看來也不夠確切,從而有時也有錯誤,例如由於沒有建立一致連續和一致收斂概念而產生的錯誤。可是關於微積分的原理,他的概念主要是正確的,其清晰程度是前所未有的。例如他關於
連續函式 及其積分的定義是確切的,他首先準確地證明了
泰勒公式 ,他給出了級數收斂的定義和一些判別法。
常微分方程 柯西在分析方面最深刻的貢獻在常微分方程領域。他首先證明了方程解的存在和唯一性。在他以前,沒有人提出過這種問題。通常認為是柯西提出的三種主要方法,即柯西-利普希茨法,逐漸逼近法和強級數法,實際上以前也散見到用於解的近似計算和估計。柯西的最大貢獻就是看到通過計算強級數,可以證明逼近步驟收斂,其
極限 就是方程的所求解。
彈性力學數學理論 柯西是在力學方面是彈性力學數學理論的奠基人。他在1823年的《彈性體及流體(彈性或非彈性)平衡和運動的研究》一文中,提出(各向同性的)彈性體平衡和運動的一般方程(後來他還把這方程推廣到各向異性的情況),給出應力和應變的嚴格定義,提出它們可分別用六個分量表示。這論文對於流體運動方程同樣有意義,它比C.-L.-M.-H.納維於1821年得到的結果晚,但採用的是連續統的模型,結果也比納維所得的更普遍。1828年他在此基礎上提出的流體方程只比現在通用的納維-斯托克斯方程(1848)少一個靜壓力項。
其他 雖然柯西主要研究分析,但在數學中各領域都有貢獻。關於用到數學的其他學科,他在天文和
光學 方面的成果是次要的,可是他卻是數理彈性理論的奠基人之一。除以上所述外,他在數學中其他貢獻如下:
1.分析方面:在一階偏微分方程論中行進丁特徵線的基本概念;認識到
傅立葉 變換在解微分方程中的作用等等。
2.
幾何 方面:開創了
積分幾何 ,得到了把平面凸
曲線 的長用它在平面直線上一些正交投影表示出來的公式。
3.
代數 方面:首先證明了階數超過了的
矩陣 有特徵值;與比內同時發現兩
行列式 相乘的公式,首先明確提出置換群概念,並得到群論中的一些非平凡的結果;獨立發現了所謂“代數要領”,即
格拉斯曼 的外代數原理。
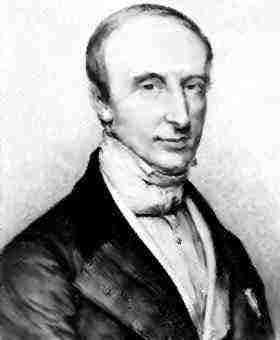 柯西畫像
柯西畫像
 德國數學家魏爾斯特拉斯
德國數學家魏爾斯特拉斯 歐拉
歐拉 柯西
柯西 費馬
費馬 巴黎爆發了反對波旁王朝的革命
巴黎爆發了反對波旁王朝的革命 路易十四一家
路易十四一家 柯西
柯西 柯西任教的巴黎大學
柯西任教的巴黎大學
 拿破崙
拿破崙