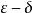基本介紹
- 中文名:極限論
- 外文名:theory of limitation
- 所屬學科:數學(微積分);經濟學
- 相關概念:無窮小,極限,微積分等
- 相關人物:維爾斯特拉斯;米都斯等
微積分的極限論,基本介紹,極限論的優越性,增長極限論,
微積分的極限論
基本介紹
極限論是數學分析的基礎,它研究極限的性質及極限存在的條件,建立求極限的法則,通過這些法則能夠利用某些簡單的變數的極限求出這些量的簡單函式的極限。
極限論中有一系列關於簡化求極限過程的定理。若 和
和 對於所有的n都有
對於所有的n都有 ,而
,而 和
和 都有有窮極限
都有有窮極限 ,則a≥b。若
,則a≥b。若 ,且存在極限
,且存在極限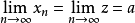 ,則
,則 亦有相同的極限,即
亦有相同的極限,即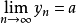 。
。







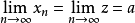

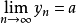
對於變數 可以實行算術四則運算,若存在有窮極限
可以實行算術四則運算,若存在有窮極限 (且b≠0),則存在有窮極限
(且b≠0),則存在有窮極限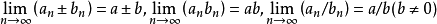 。若
。若 或
或 , 則分別有
, 則分別有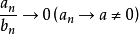 和
和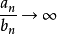 ,若兩序列同時趨向於0或
,若兩序列同時趨向於0或 ,則分別稱
,則分別稱 為不定型
為不定型 和
和 ,要確定不定型,也就是確定
,要確定不定型,也就是確定 的極限,可以採用不同的方法,最一般而簡便的方法是洛必大法則。
的極限,可以採用不同的方法,最一般而簡便的方法是洛必大法則。


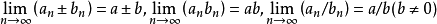


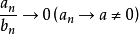
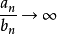





若 ,而
,而 ,則
,則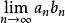 是
是 型不定型,若
型不定型,若 ,則其差的極限
,則其差的極限 叫做
叫做 型不定型。
型不定型。


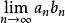




極限論還建立了極限存在準則(收斂準則),若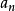 單調不減
單調不減 ,並有上界
,並有上界 ,則
,則 存在(若
存在(若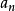 無上界,則當
無上界,則當 時
時 ),對於單調不增而有下界的序列亦有類似結論。在一般情況下,序列xn有有窮極限的充要條件是對於任意小的ε>0,存在著正整數N,當n>N,n'>N時,不等式
),對於單調不增而有下界的序列亦有類似結論。在一般情況下,序列xn有有窮極限的充要條件是對於任意小的ε>0,存在著正整數N,當n>N,n'>N時,不等式 成立(柯西-波爾查諾定理),換句話說, 當變數xn的角碼增大時,其值就彼此無限地接近起來。
成立(柯西-波爾查諾定理),換句話說, 當變數xn的角碼增大時,其值就彼此無限地接近起來。
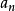



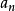



在極限論中還研究序列 ,其中各項是從已知的xn中取出的, nk——遞增的某自然數序列:
,其中各項是從已知的xn中取出的, nk——遞增的某自然數序列: 這裡取所有自然數值的角碼已不是n, 而是k;當
這裡取所有自然數值的角碼已不是n, 而是k;當 時,
時, ,這個序列
,這個序列 叫做部分序列。
叫做部分序列。





若原序列有極限,則其部分序列亦有相同的極限,對於任一有界序列總可以找出具有有窮極限的部分序列(波爾查諾-維爾斯特拉斯原理),這個極限稱為已知序列的部分極限(或聚點),總存在有最大的部分極限( 和最小的部分極限(
和最小的部分極限( ),若
),若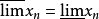 ,則xn有極限(通常意義下的極限),它們的相同的值就是極限值。
,則xn有極限(通常意義下的極限),它們的相同的值就是極限值。


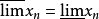
上述關於變數xn(數值序列)的所有基本概念都可以推廣到函式上去。當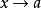 時
時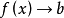 的充要條件是:對於以a為極限的任一數值序列
的充要條件是:對於以a為極限的任一數值序列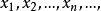 ,所對應的函式值序列,即數值序列
,所對應的函式值序列,即數值序列 ,…有其自己的極限b。
,…有其自己的極限b。
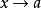
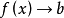
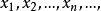

微積分概念的基本原理屬於無窮小問題,但並非“無窮小”世界的全部,如果已經認清了無窮小,自然對建立微積分遊刃有餘,反之,若僅從微積分概念的需要出發,則並不需要完全地認清“無窮小”,只需極限論即可。
亦即無窮小認識對於建立微積分的需要來說是充分的,但並非必要,當然,這點只是個認識性結論,僅是建立在實際觀察基礎上的,並沒有嚴格的邏輯證明,事實上,從當初極限論的誕生能折服整個科學界這點,加上逾一個世紀的科學實踐檢驗,我們有理由相信,它對於微積分學的基礎來說已是足夠的,因此單純從微積分角度說,極限論應該是值得肯定的。
但我們這裡是以完全地認識“無窮小世界”為目標,那么,在此標準下即可發現,極限論是不能代替無窮小認識的,因而相對來說,它是有缺陷的。
極限論的優越性
1.極限論給出了又一種用有限去表述無窮的方法
周期是自然界廣泛存在的一種典型的用來表現無窮的有限形式,因此其理論也十分重要且廣泛。那么,極限論包括無窮級數形式研究可算是另一種用有限來表征無窮的形式,甚至還是用以獲得無窮結論的手段。這是十分了不起的。
2.極限論帶來了微積分方法的“算術化”
由於極限的(公理化)定義來得簡練而確切,致使由它建立起來的微分、積分定義也來得簡練明快,沒有繁複之感,以致整個微積分方法之容易掌握和運用,被科技界公認為“算術化”了的方法,它完全可以被列為算術第九則、十則運算,歸根結底這是極限概念之簡練性獲得的效果。
3.極限論在微積分學上的實用效果是成功的
因為百餘年來甚至說300餘年來對微積分學激烈的研究,已經是對極限定義的一個嚴格檢驗過程。或可以說,幾百年來,微積分學已被研究得相當成熟,儘管今天在初等微積分範圍內還有論文,但已看不到突破性、基礎性成果了,一個學科能達到這種狀態已算是成熟的了,但是,卻一直未發現在微積分意義下極限概念有什麼不足。
不過必須指出,只能說是從微積分學來講,極限論是成功的、完備的,不過將看到,若超出微積分概念,直接針對無窮小的認識,極限概念則顯得遠遠不足了。
增長極限論
增長極限論又稱“零增長理論”、“經濟成長有限論”。是1972年由美國學者梅多斯(D.L.Mea-dows)等人在為羅馬俱樂部所寫的名為《增長的極限》的報告中對經濟成長提出的一種觀點。羅馬俱樂部是1968年4月由知名科學家、經濟學家、社會學家等組成的一個研究團體,旨在研究資源、環境、人口等“人類困境”問題。第二次世界大戰後,西方主要資本主義國家運用凱恩斯經濟理論,實施國家干預主義政策,在使經濟出現持續、高速增長的同時,也帶來了資源的迅速消耗及生存環境的惡化。該報告認為:工業化的結果必然造成對自然和生態的極度破壞。只有當人口和工業投資都停止增長時,才能在世界範圍內實現真正的經濟均衡。他們把經濟成長所帶來的各種矛盾和問題歸結為相互影響的五種因素,即人口增長、農業生產、資源消耗、工業投資和環境污染。根據當時的資源條件和發展速度,這五種因素都呈指數增長,因此是難以為繼的。他們綜合考察這五種因素,並編成一組全球模型進行模擬計算,得到的結果是:1970年以後,人口和工業仍維持著指數增長,但迅速減少的資源將限制這種增長。工業化達到最高點後,人口和環境污染還會繼續增長;但由於糧食缺乏、環境污染,最後人口也將停止增長。預計2100年到來之前,全球就會停止增長,社會因此而崩潰。其結論是,為避免此類情形的發生,必須在1975年之前停止人口增長,1990年之前停止工業投資增長,以達到零增長的全球性均衡狀態。他們歸納的使人口和工業投資都停止增長的辦法是:(1) 每年的人口出生率應等於預計的死亡率,(2) 每年的投資率應等於折舊率。零增長理論提醒人們必須關注經濟成長與環境污染、資源利用、世界人口增長等問題的相互關係,綜合考慮各種因素的影響。當然,這只是一種警示性的理論,其結論也過於消極悲觀。
極限論的思想方法同於生態學中的 “環境容量” 概念。環境容量是指生物種群增長的上限,達到上限時種群停止增長。米都斯等人認為社會經濟發展也有類似的規律。所謂 《增長的極限》,實指社會經濟發展的環境容量。極限論雖然深刻地揭示了經濟成長同環境的對立關係,但否認科學技術和經濟發展的調節機制可以改變環境限度;雖然正確地看到地球環境容量是人口和經濟成長的限制因素,但沒有看到這種限制因素是促進人類開發新資源、新技術和改進經濟模式、改革社會關係的強制性推動力量,沒有看到人與環境的衝突也是人類社會發展的動力之一 。極限論是悲觀主義的環境理論。