電漿診斷

電漿診斷（plasma diagnostics）是根據對電漿物理過程的了解，採用相應的方法和技術來測量電漿參量的科學技術。電漿物理現象要用多個參量才能描述，就像醫生對病人的病情要作多方面的診斷後方可確診一樣。因此，借用醫學中的“診斷”一詞，將電漿參量的測量稱為電漿診斷。

電漿診斷是用實驗方法測定電漿參量的技術。診斷的方法有探針法、微波法、雷射法、光譜法、光學法和粒子束法，其中粒子束法的套用不如前五種普遍。診斷的參量包括微觀參量（如碰撞頻率）和巨觀參量（如密度、溫度、壓力等熱力學參量，以及粘性、擴散、熱導率和電導率等輸運係數）。一般表征部分電離電漿特性的參量主要是電子密度、電子溫度和碰撞頻率。電子密度和電子溫度的範圍不同，所用的測量方法也不同。

基本介紹

• 中文名：電漿診斷
• 外文名：Plasma diagnostics
• 學科：電漿物理學
• 適用範圍：電漿

電漿診斷是用實驗方法測定電漿參量的技術。診斷的方法有探針法、微波法、雷射法、光譜法、光學法和粒子束法，其中粒子束法的套用不如前五種普遍。診斷的參量包括微觀參量（如碰撞頻率）和巨觀參量（如密度、溫度、壓力等熱力學參量，以及粘性、擴散、熱導率和電導率等輸運係數）。一般表征部分電離電漿特性的參量主要是電子密度、電子溫度和碰撞頻率。電子密度和電子溫度的範圍不同，所用的測量方法也不同（圖1、圖2）。

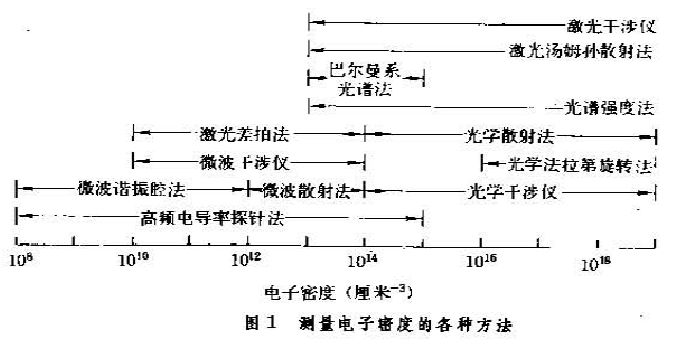
圖1 測量電子密度的各種方法

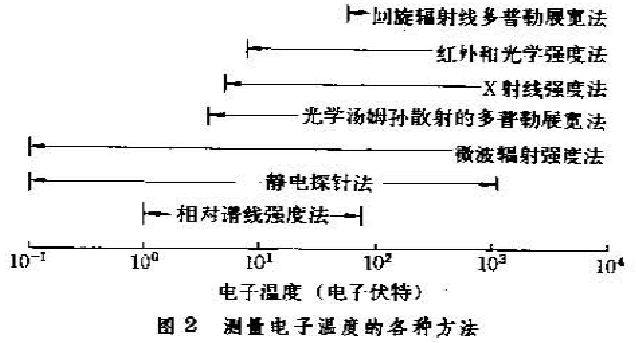
圖2 測量電子溫度的各種方法

診斷技術起源

電漿診斷技術是隨著電漿科學的進展而發展起來的。電漿診斷源自光學天文的觀測。從測量恆星發射可見光的天文觀測開始，現已發展成為包括射頻電磁波、紅外線、紫外線、X射線、γ射線以及各種粒子在內的天體電漿診斷。電漿診斷是天體測量學和天體物理學的一個重要基礎。19世紀以來，氣體放電的研究促進了實驗室電漿診斷的發展。核爆炸試驗、高空飛行器和航天技術、無線電技術，推動了電漿診斷學的發展。特別是20世紀中葉以來，受控熱核聚變的研究，進一步促進了電漿診斷技術的發展。

診斷方式

電漿的診斷可分為被動方式和主動方式兩大類。被動方式的診斷是指通過測量電漿自身發射的電磁波或粒子來獲得有關電漿參量的測量方式。電漿發射的電磁波有很寬的頻譜範圍，從微波、遠紅外、可見光、真空紫外，直到軟X射線和硬X射線。引起輻射的機制有軔致輻射、迴旋輻射、複合輻射、線輻射及集體過程引起的輻射等。這些輻射提供了有關電子溫度、離子溫度、離子或中性粒子成分、粒子速度分布等各種信息。從電漿中還發射出各種粒子，如電荷交換產生的中性粒子、聚變產生的中子等，對這些粒子的測量可得到有關離子溫度等信息。此外，還可測量電漿的一些電磁信號，如電壓、電流、磁場等。還可將探針直接插入電漿進行測量。如靜電探針可測量局部的電子密度、溫度、電位場等；磁探針可測量電漿中的局部磁場。主動方式的診斷是指通過由外部輸入的電磁波、粒子束等來測量電漿參量的測量方式。如用電磁波散射法研究電離層；由雷射散射法可測定實驗室電漿的電子溫度和電子密度分布；由微波干涉法或雷射干涉法可測電子密度分布；由中性粒子束的衰減可測量密度；由雷射誘導螢光測量電漿不同成分的密度、溫度、速度分布；由重離子束可測量電子密度分布、磁場分布、電勢分布等。

測量範圍

同一種電漿參量可用不同的測量方法測量，以便相互印證。各種測量方法有其不同的適用範圍，如測量離子溫度的方法有線光譜的都卜勒寬度、電磁波的集體散射、高能中性粒子能譜分析、聚變中子測量等方法。一般高溫時可用中性粒子或中子測量來測定離子溫度，低溫低密度時可用都卜勒寬度來測定離子溫度，低溫高密度時可用集體散射方法來測出離子溫度。

電漿診斷是集物理學和技術科學為一體的技術。通過對電漿物理過程的理解來確定要測的電漿參量並選定適用的測量方法；測得的結果又需要用電漿物理知識加以分析，揭示測量結果所反映的物理現象。

診斷方法

電漿診斷技術是隨著電漿科學的進展而發展起來的。20世紀初，開始觀測宇宙電漿。20年代，為了研究氣體放電，開創了實驗室電漿診斷。從50年代起，在受控熱核反應和空間技術研究的推動下，電漿診斷的研究進入全盛時期。下面將電漿診斷套用的各種方法作一介紹。

探針法

將實體探針放入電漿中以獲得所需參量，是電漿診斷的基本手段之一。此法可以得到有關電漿內部細緻結構的信息和各種參量的分布情況。缺點是會干擾被測電漿，例如改變流動圖像，形成空間電荷包鞘，產生雜質污染等。此法套用的探針及其探測原理分述如下：

靜電探針 它是一種金屬電極。圖3是三種典型靜電探針結構的剖面圖。通過電路圖4如將偏置電壓加在探針和補償電極（如電漿的金屬器壁或放電電極等）之間，探針就從電漿中收集帶電粒子，形成電流。用適當的儀表記錄下電壓和電流，便可得到探針的電流－電壓特性（伏安特性）曲線（圖5）。

圖3 靜電探針結構（剖面圖）

圖4 靜電探針測試電路

圖5 靜電單探針的伏安特性曲線

特性曲線可以分為三個不同特點的區域：①飽和離子電流區：探針電位遠低於電漿的空間電位，探針基本上只收集正離子。②過渡區：探針電位逐漸增高，但仍低於空間電位，探針同時收集電子和正離子。當電子電流和離子電流相等時，探針總電流為零，相應的探針電位稱為浮置電位。以上兩個區的特性統稱為“負探針特性”。③飽和電子電流區：當探針電位等於空間電位時，帶電粒子完全憑藉本身的熱運動到達探針表面，因此探針收集的是無規電流。由於電子質量遠小於離子質量，電子的無規電流遠大於離子無規電流。探針電位高於空間電位時，幾乎全部離子都被拒斥，探針只收集電子電流。

靜電探針理論給出電漿參量和探針特性之間的定量關係。利用靜電探針可以測量電漿中帶電粒子（電子或離子）的數密度、電子溫度以及空間電位等。移動探針還可以測知上述參量的分布情況。

靜電探針法是I.朗繆爾等人在研究低氣壓氣體放電時創製的，現在已在高氣壓、高溫、有流動、有磁場等各種複雜情況中得到廣泛的套用。

磁探針。它是一個探測線圈。當其中的磁通量發生變化時，線圈中便產生感應電動勢，從而給出電漿中當地磁場的時間變化率。如在探針輸出端接上積分電路，便可直接得到磁感應強度。若改變探針線圈取向可以測得磁場在不同方向上的分量。根據這些數據，還可以推算電漿中的電流和電場分布、壓力分布以及電導率等。磁探針一般只能用於探測隨時間變化的電漿。磁探針輸出信號一般很弱，要避免雜散拾音，最好採取靜電禁止措施。

圖6 磁探針結構

圖7 電導率計在激波管中的套用

圖8 射頻電導率探針

電導率探針。由磁場線圈和探測線圈組成（圖6）。它利用磁場和電漿相互作用原理來確定電漿的電導率。電導率探針有電導率計（圖7）和射頻電導率探針（圖8）等類型。對於電導率計，當高速運動的電漿切割其磁場線圈的磁力線時，電漿中便產生感應電流。這又在探測線圈中造成磁通量的變化並感生出電動勢。在已知電漿運動速度的情況下，測量探測線圈中的感應端電壓，可以得到電漿的電導率。射頻電導率探針是把磁場線圈和探測線圈合成一個。它利用振盪器產生高頻振盪，並通過電介質視窗傳輸到電漿中，從而感應出渦流，渦流又影響線圈的阻抗。測量線圈的品質因數（Q值）或諧振頻率的變化，可以確定電漿的高頻電導率。

微波法

利用電磁波頻譜中的微波與電漿相互作用的原理來測量電漿參量的方法。微波在電漿中傳播時，會使微波器件的工作狀態發生變化（如Q值下降等），並發生吸收、相移以及反射、折射、散射等過程。相應的衰減量、相移量和反射量等物理量可由實驗測定，而它們對電漿的電子密度、碰撞頻率等參量的依賴關係則可由理論分析給出。基於這類現象的診斷稱為微波傳輸測量，它分為空腔法和自由傳播法兩種。自由傳播法有三種基本方法（圖9），可進行衰減測量、反射測量和相移測量等。另一類微波法是測量電漿的微波輻射（如黑體輻射、軔致輻射、迴旋輻射和相干輻射等），從而獲得有關電漿溫度、不穩定性等特性的信息。

圖9 微波傳輸測量自由傳播法示意圖

微波法的優點是不干擾被測電漿，缺點是空間回響較差，動態範圍較小。常用的微波測試設備有：

微波諧振腔 可以傳輸微波的波導或諧振金屬腔，用於空腔法。當微波穿入封閉於腔內的電漿中時，電漿的特性會影響諧振腔的狀態，例如品質因數Q值下降、諧振頻率移動等。通過擾動分析等方法又可以得知諧振腔Q值變化、頻移與電漿參量之間的關係。由此可以測出電漿的電導率、電子密度和碰撞頻率等參量。如果電漿的電子密度過高，體積過大，此法即不適用。

微波干涉儀 一種基於橋式電路的微波裝置，用於自由傳播法。它主要是利用相移法進行測量，特別適宜於觀測瞬變電漿，但同時也可測定傳輸信號的衰減量，因此套用相當廣泛。在干涉儀中，微波信號分成兩路：一路通過電漿，當測量路徑中的電漿參量發生變化時，此路信號的相位便發生相應的變化；另一路為參考路徑，其中的相移是固定不變的。這兩路信號在適當的微波器件（如T形接頭、耦合器等）上疊加混合，便發生干涉。干涉後的信息由檢測器等器件檢測，輸出並在示波器等儀表上顯示。干涉儀的回響主要取決於相移，但與振幅的衰減也有關係。微波干涉儀可以給出電漿的電子密度、碰撞頻率以及這些參量的剖面分布等信息。

雷射法

用雷射作為光源、激發源或探測器來診斷電漿參量的方法。雷射診斷的優點是：對電漿干擾小，空間解析度和時間解析度高，可診斷的電漿電子密度範圍寬（10—10）厘米，溫度範圍大（10—10開），特別是對非熱平衡電漿的診斷優於光譜法等診斷方法。因此雷射診斷成為電漿診斷，特別是高溫度、高密度電漿診斷的主要手段。雷射法有下述幾種：

雷射干涉法。雷射具有功率大、亮度高、單色性好、方向性強和偏振度好等優點，是十分優良的相干光源。用它作馬赫－曾德爾干涉儀、邁克耳孫干涉儀等一般光學干涉儀的光源，可使干涉儀易於調節，使用方便。有些新型干涉儀其中作光源的雷射器兼作探測器，因而結構簡單，靈敏度高。雷射干涉法可以直接測量電漿的折射率，並確定電漿的密度和溫度等參量。常用的雷射干涉法如下：

①標準干涉法，又稱雙光束干涉法。設備為馬赫－曾德爾干涉儀（原理如圖10所示）。此法是將一束雷射用半反射鏡等分成兩束相干光，然後再使兩束光匯合，由於它們經過的光程不同，產生相位差，形成明暗相間的干涉條紋，稱為背景條紋。當其中一束光通過待測的電漿（其光程與電漿的折射率有關）同另一參考光束再匯合時，會產生附加的光程差，使干涉條紋發生變動。把干涉條紋和背景條紋進行比較，讀出條紋移動數目，就能確定電漿的折射率。根據電漿折射率同電子密度的關係，可推算出在光束經過的電漿長度內的平均電子密度。這種方法能診斷的電漿電子密度下限約為10厘米。

②耦合腔干涉法，又稱三鏡片干涉法（原理如圖11）。設備為雷射干涉儀。干涉儀中的反射鏡M₁和M₂構成氣體雷射器的諧振腔；反射鏡M₂和M₃構成參考諧振腔，其中放入待測的電漿。雷射器的光從M₂透射到參考腔，通過電漿被M₃反射後又透過M₂回到雷射器中。如果經過M₃反射的光和直接從M₂反射的光是同相位的，則雷射器輸出強度增加，如果兩者相位不同，輸出強度便減小。因此當電漿折射率變化（由電漿密度變化引起）時，雷射器的輸出強度被調製。光兩次通過參考諧振腔，電漿中的光程每改變二分之一波長就會使雷射輸出強度發生一個條紋的變化。在這種雷射干涉儀中，干涉條紋的移動數N與電漿折射率n的關係為：

式中λ為入射雷射波長；L為雷射通過的電漿長度。

雷射器在雷射干涉儀中既作光源，又作探測器，所以雷射干涉儀結構簡單，靈敏度高。這種干涉儀能測定電子密度及其隨時間的變化，尤其適用於脈衝放電電漿的診斷。耦合腔干涉法可以測量的電子密度下限通常約為10厘米，經改進後可達10厘米。

③差拍干涉法。將待測電漿放入雷射器的諧振腔內，電漿密度的變化引起光程的變化，諧振腔的振盪模式也發生相應的變化，從而又引起雷射器輸出頻率的變化。用差拍技術或外差方法測定這種微小的頻率變化，就能確定電漿的電子密度。此法僅適用於測量慢變化或穩態的電漿，並要求雷射系統十分穩定。此法可以測量的電子密度範圍約為10—10厘米。

④雙波長干涉法。採用兩束不同波長的雷射同時通過待測電漿，產生兩組不同波長的干涉條紋，可同時測定電漿中電子和原子兩種組分的密度。單波長干涉法只考慮電子而忽略離子、原子等重粒子對電漿折射率的影響。如果要更準確地測定電子密度和原子密度，則須採用雙波長干涉法。

圖10 馬赫-曾德爾干涉儀原理圖

圖11 雷射干涉儀原理圖

雷射散射法。此法可用來測定電漿的電子溫度、密度、離子溫度及其空間、時間分布。常用的方法如下：

①湯姆孫散射法。強雷射通過電漿時，如果散射光波長遠小於德拜長度，則雷射散射受單個電子無規則熱運動的影響，而不受電子和離子整體運動的影響，因而散射譜僅能反映電子運動效應。根據實驗測出的散射譜的半寬度就能求出電漿的電子溫度。電子散射譜半寬度（半高度上的全寬度），可以分別用圓頻率或波長表示，如下：

式中w_o為入射光圓頻率；λ₀為人射光波長，θ為散射角；k為玻耳茲曼常數；T_o為電漿的電子溫度；m為電子質量；c為真空光速。

②集合散射法。強雷射通過電漿時，如果散射光波長遠大於德拜長度，則雷射散射主要受電子和離子整體運動的影響，散射譜就能反映離子運動效應。根據實驗測出的離子成分譜，就可以估算離子溫度。由於散射截面十分微小。（一般為10~10厘米的量級），而散射信號強度的量級僅為入射信號強度的10，為了能夠測出散射信號而且有較小的統計誤差，必須採用大功率巨脈衝雷射器作光源，採用靈敏度高、信噪比大、時間回響快的光探測器作接受器。

③喇曼散射法。強雷射通過氣體或電漿時，有一部分散射光的頻率會發生變化，出現頻率為v±Δv的譜線。頻移Δv對應於氣體或電漿中的分子、原子系統的振動能量和轉動能量，由此可以獲得原子、分子的振動溫度、轉動溫度、密度和能級分布等。喇曼散射光譜強度十分微弱，用一般光源難以觀測，直到雷射器出現後，喇曼散射法才迅速發展起來。

雷射散射法的優點是能在不擾動電漿的情況下，測定電漿的局部參量，空間解析度可以達到0.5毫米以下，時間解析度可以達到幾十納秒。

光譜法

利用電漿的發射光譜或吸收光譜診斷電漿溫度、密度和化學組分等參量的方法。此法是在50年代初期由H.邁克等人較為系統地提出的，起初套用於天體物理和基礎實驗研究，後來又套用於航天環境模擬、化工冶煉、熱加工和能源等方面的實驗中。60年代，開始用雷射光譜診斷法（吸收光譜法、螢光光譜法、喇曼光譜法、光聲光譜法等）對電漿狀態和輸運性質進行實驗研究。下面只介紹較為常用的、成熟的經典的光譜測量溫度的方法。

通常的光譜法測溫，總是假定電漿處於局部熱力學平衡和光薄狀態。所謂局部，應理解為“巨觀上足夠小，微觀上足夠大”的區域。“巨觀上足夠小”系指電漿雖在一個大區域內處於非均勻態（例如各點的溫度不一樣），但如把大區域劃分為若干個小區域，在每個足夠小的區域中，溫度、壓力等又可近似看作是均勻的。“微觀上足夠大”系指在每個巨觀上足夠小的區域裡包含足夠多可作統計估算的粒子。所謂光薄，應理解為電漿相當稀薄，不存在自吸收作用（自吸收系指電漿中原子或離子的輻射通過整個等離子區域時，被同一元素的另一些原子或離子所吸收）。 光譜法測量通常是通過測量譜線強度、譜線的位移和加寬或連續譜的強度來得到所要的電漿參量。光譜法測溫可分為譜線加寬法、相對強度法、絕對強度法、譜線反轉法、連續譜法、離軸峰值法等。

譜線加寬法測溫。譜線加寬的原因較多，但在加寬原因比較單一的條件下可採用這種方法測溫。譜線加寬法測溫分為：

①都卜勒加寬測溫。只適用於粒子數密度較小、低壓、稀薄氣體的情況，譜線加寬主要是由都卜勒效應引起的。都卜勒加寬測溫的公式為：

式中T為熱力學溫度（開）；Μ為電漿氣體分子量（克）；λ₀為加寬譜線的中心波長（埃）；Δλ_1/2為所測加寬譜線輪廓的半寬度（圖12）。從上式可知，溫度愈高，都卜勒加寬愈大，而在相同溫度下，輕粒子的譜線加寬大於重粒子的，故此法常採用氫譜線作為測量線。在低溫電漿測溫範圍內，加寬量很小，僅為0.1—0.001埃，必須用高解析度光譜儀才能測定。

圖12 加寬譜線輪廓的半寬度

②斯塔克加寬測溫。外電場、電漿的本身電場和變化電場都會引起譜線變寬或峰值位移。此法適用範圍是：電子數密度為10—10厘米，壓力約一個大氣壓左右，溫度為10—2×10開。

相對強度法測溫。此法是根據同類原子（或離子）兩譜線的輻射密度（或發射係數）之比和溫度的基本關係式推導出溫度，即：

式中

為從高能級i向低能級m躍遷時，頻率為 的輻射發射係數；

為從高能級j向低能級l躍遷時，頻率為的輻射發射係數； 、 分別為從i能級向m能級和從j能級向l能級的白髮躍遷幾率; 、 分別為第i、j能級的統計權重； 、 分別為第i、j能級的能量,k為玻耳茲曼常數，數值為1.380662×10（焦耳/開）;T為激發溫度；h為普朗克常數; 為單位體積內全部原子（或離子）數，即粒子數密度；u為原子（或離子）的微觀狀態和。

圖13 光譜測溫光路原理示意圖

實際上，由於電漿源溫度分布很不均勻（溫度梯度高達每毫米幾千開），其熱物理狀態不能單用一個“溫度”來表征，所以需要測量溫度的空間分布。常用的方法有空間掃描法、光譜掃描法、局部區的光學隔離法等。用經典光譜儀測溫常採用空間掃描法。在光譜儀焦平面上取出兩譜線的輻射能量，經傳光光導纖維束進入光電倍增管PMT，由數字儀表顯示記錄。

在軸對稱電弧電漿射流一側測出的信息是實測方向輻射率的疊加效應。空間掃描法是基於測量電漿一側一系列橫向的光譜輻射率，通過一定轉換就可算出軸向位置不同的各橫截面上溫度的徑向分布，並可繪出整個電弧電漿射流的溫度分布圖。選測的兩譜線，宜選用能級差較大的線對，以利於提高測試的精度。

絕對強度法測溫。此法測溫的基本關係式為：

式中A_im、G_i、u、E_i，對確定的原子（或離子）有確定的數值，E₀由薩哈方程和分壓定律計算得到。因此，測得某一譜線（例如氫離子、氮離子或氬離子譜線）的輻射率，把它換算成為發射係數ε，可以根據測溫的基本關係式計算出相應的溫度。

譜線反轉法多用於3000開以下火焰透明電漿溫度的測量。連續譜法用於測量10開以上電漿的溫度。但在這種高溫條件下，產生連續譜的原因較多，難以確認，常會引起較大的測量誤差。離軸峰值法主要用於測量2.6×10開以上氬電漿的溫度和1.6×10開以上的一次電離譜線。

光譜法具有非接觸測試的特點，是低溫電漿診斷的重要方法之一。其測試系統如配置微處理機，就可實現測試和數據處理過程自動化，並提高測試診斷水平。

參考資料

M.Venugopalan,ed,Reactions under Plasma Conditions,V.2.John Wiley &Sons, New York, 1971.

H.T.Richard.Spectroscopic Gas Temperature Measure-ment (Pyrometry of Hot Gases and Plasma).E1sevier,Amsterdam, 1966.

W. Lochte-Holtgreven,ed,Plasma Diagnostics, North-Holland Pub.Co, Amsterdam, 1968.