基本介紹
- 中文名:羅巴切夫斯基幾何
- 外文名:Lobachevskian geometry
- 又稱:雙曲幾何
- 模型:龐加萊模型,克萊因模型
- 發現者:羅巴切夫斯基
簡介
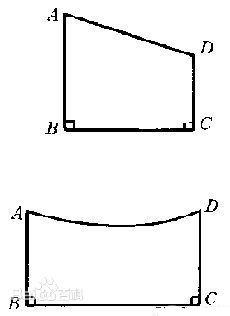
模型
龐加萊模型

羅氏幾何一般指本詞條


公理、定義及基本概念均相同. 人們把這兩個幾何系統中的相同的部分(即一切相同的公設、公理、定義及基本概念)所構成的幾何系統稱為絕對幾何.故歐氏幾何由絕對幾何外加第五公設構成,而羅氏幾何由絕對幾何外加羅氏公設構成.因此,羅氏幾何...
在這種幾何里,羅巴切夫斯基平行公理替代了歐幾里得平行公理,即在一個平面上,過已知直線外一點至少有兩條直線與該直線不相交。由此可演繹出一系列全無矛盾的結論,並且可以得出三角形的內角和小於兩直角。羅氏幾何中有許多不同於歐氏幾何的...
幾何公理系統的解釋是19世紀中葉隨著羅氏幾何的產生而發展起來的,貝爾特拉米(E.Beltrami)利用他的微分幾何模型,龐加萊(((J.-)H.Poincaré)利用他的複數平面模型,克萊因((C.)F.Klein)利用他的射影幾何模型等,各自成功地解釋了羅氏...
其中一個有趣的問題是,非歐氏幾何中過直線外一點的平行線可以無窮。不久之後,俄國的一位著名數學家也發現了一個新的非歐幾何,即羅氏幾何。他的三角形內角和是小於180度的。而19世紀初非歐式幾何的發現,正是後來愛因斯坦發現廣義...
絕對幾何指滿足希爾伯特Hilbert的《幾何基礎》中的接合公理、順序公理、契約公理和連續公理等四組公理的幾何。歐式幾何就是在滿足這四組公理的基礎上還滿足平行公理,而羅氏幾何(非歐幾何的一種)就是在這四組公理的基礎上還滿足...
俄羅斯數學家羅巴切夫斯基用“在同一平面內,過直線外一點可作兩條直線平行於已知直線”代替第五公設,由此導出了一系列新結論,如“三角形內角和小於兩直角”、“不存在相似而不全等的三角形”,等等,後人稱為羅氏幾何學。德國數學家黎曼...
5 幾何學的統一與公理化思想 5.1 幾何學的統一 5.2 幾種幾何學的比較 5.3 公理化思想方法 6 幾何學的近現代發展簡介 6.1 微分幾何 6.2 拓撲學 練習1 第2章 非歐幾何的幾種典型模型 1 銳角假設與羅氏幾何 1.1 銳角假設...
4.3非歐幾何的發展與確認 5幾何學的統一與公理化思想 5.1幾何學的統一 5.2幾種幾何學的比較 5.3公理化思想方法 6幾何學的近現代發展簡介 6.1微分幾何 6.2拓撲學 練習1 第2章非歐幾何的幾種典型模型 1銳角假設與羅氏幾何 1...
第11次印刷成都翻刊本徐樹勛就將其改名為《續幾何》。直至20世紀中期,已鮮有“形學”一次的使用出現。分支學科 平面幾何 立體幾何 非歐幾何 羅氏幾何 黎曼幾何 解析幾何 射影幾何 仿射幾何 代數幾何 微分幾何 計算幾何 拓撲學 ...
等距曲面(equidistant surface)簡稱等距面。羅氏空間的三種基本曲面之一。指在羅氏空間中,在給定平面a的同一側,到a的距離相等的點的軌跡。羅氏幾何是羅巴切夫斯基幾何的簡稱。非歐幾何的一種,亦稱“雙曲幾何學”。是俄國數學家羅巴切夫斯基...
龐加萊模型(Poincare's model)一種羅氏幾何模型。第一個在歐幾里得幾何系統中構造出羅巴切夫斯基幾何公理系統模型的是法國數學家龐加萊(Poincaré,(J.-)H.),由於該模型與非歐幾何的相容性問題以及如何解決第五公設問題等直接相關,從而...
羅氏幾何是第一個被提出的非歐幾何學,它的基本觀點是: 第一,第五公設不能被證明; 第二,可以在新的公理體系中展開一連串推理,得到一系列在邏輯上無矛盾的新的定理,形成新的理論。羅氏幾何學的公理系統區別於歐式幾何學之處,僅僅...
羅巴切夫斯基函式(Lobachevskian function)簡稱羅氏函式,羅氏幾何中的重要函式關係。在羅氏平面上,若∠BAP是線段AB的平行角,d(AB)=x,μ(∠BAP)=α,則函式:α=π(x)稱為羅巴切夫斯基函式。羅巴切夫斯基函式是嚴格單調遞減的連續函式...
龐加萊複數平面模型(Poincaré complex plane model)是解釋羅氏平面幾何的模型。這個模型是龐加萊((J.-)H.Poincaré)首先提出來的,因為該模型的點是在複數上半平面上,所以稱之為羅氏幾何的龐加萊複數平面模型。龐加萊利用這個模型,...
最後一本用俄、法兩種文字寫的《泛幾何學》,在他逝世前一年(1855)發表。人物評價 羅氏幾何的創立沒有及時引起重視,直到他去世後12年(1868)義大利數學家E.貝爾特拉米證明了在歐氏空間的偽球面上可以實現羅巴切夫斯基平面的幾何學,這樣...
羅氏幾何的創立對幾何學和整個數學的發展起了巨大的作用,但一開始並沒有引起重視,直到羅巴切夫斯基去世12年後才逐漸被廣泛認同。羅巴切夫斯基在數學分析和代數學方面也有一定成就。個人事跡 1893年,在喀山大學樹立起了世界上第一個為數學家...
作為絕對形,關於實二階曲線k的自同構變換稱為雙曲射影運動。具有公共絕對形的雙曲射影運動的全體構成射影變換群的一個子群,稱為雙曲運動群。研究在雙曲運動群下不變性質與不變數的幾何稱為雙曲幾何,或稱羅氏幾何。群 群是一種...
黎曼幾何作為非歐幾何的一種,它與羅巴切夫斯基幾何相比,有著實質性的不同。羅氏幾何主要工作是建立了一整套區別於歐幾里得的《幾何原本》的邏輯體系; 而黎曼幾何的核心問題是以微分幾何為基礎,建立曲線坐標系中的微分方法。羅氏幾何是第...
羅巴切夫斯基平行公理(Lobachevskian axiom of parallels)是羅巴切夫斯基幾何中最重要的公理,簡稱羅氏平行公理。即存在直線a及不在a上的一點A,過A點至少有兩條直線與a共面且不相交,羅氏平行公理是歐氏平行公理的反面命題。公理介紹 公理1...
貝爾特拉米映射是球面到平面的一種特殊映射。這個映射是貝爾特拉米 (Beltraim,E.)在研究羅氏幾何時首先提出來的,稱為貝爾特拉米映射。簡介 貝爾特拉米映射是球面到平面的一種特殊映射。在空間直角坐標系中,取一個半徑為 a 的球面,設球心...
羅巴切夫斯基公設(Lobatchevsky's postulate) 簡稱羅氏公設。定義 羅巴切夫斯基公設(Lobatchevsky's postulate) 簡稱羅氏公設.羅氏幾何術語.指羅巴切夫斯基平行公理.即過平面上任一已知直線外的任一點,至少能引兩條直線與該已知直線不相交.可知...
射影測度是凱萊(A.Cayley)於1859年建立的,1871年,克萊因(C.F.Klein)利用射影測度的概念來說明非歐幾何學。非退化的二階曲線有實虛兩種情況,若絕對形為非退化的實二階曲線,則可構成羅氏幾何;若絕對形為非退化的虛二階曲線,則...
偽球面是一種形如喇叭的特殊曲面,其高斯曲率為負常數的特殊曲面。具體而又是在,偽球面的內蘊幾何與羅氏幾何是一致的,一個偽球面可以解釋成為羅氏幾何中一個平面的一部分。這就為羅氏幾何提供了一個模型。這就是說,非歐幾里得幾何命題...
等傾割線(isoclinal secant line)是羅氏平面上的基本曲線之一,與共面二直線a,b相交成相等的同側內角的直線,稱為二直線a,b的等傾割線。在羅氏平面上,共面二直線有相交、平行、離散三種位置關係,過一直線上一定點都存在等傾割線AB...
過截角超無限邊形鑲嵌是一種雙曲面鑲嵌,由正方形和超無限邊形構成,是歐氏鑲嵌,截角無限階二邊形鑲嵌在羅氏幾何中的一個類比。該幾何圖形也可以視為是一種“發散”的柱體,由於其可以類比自無限角柱,是指底面是無限邊形的柱體,...
後來,龐卡萊(Poincare`,1854-1912)在歐氏半平面上構造了羅氏幾何的模型,把羅氏系統的相容性證明通過一個模型化歸為歐氏系統的相容性證明,但卻由此導致了人們對歐氏系統相容性的重重疑慮。幸虧那時已經有了解析幾何,這就等於在實數系統...
極限球面(horosphere)是羅氏空間的三種基本曲面之一,指在羅氏空間中,從直線a的一個點A,到在確定方向上與a平行的任意直線引等傾割線,其端點的幾何軌跡。點A也是極限球面上的點,直線a及與a在同方向平行的直線稱為極限球面的軸線,...
G宇宙模型是研究天文物理學的一門學問。非歐宇宙 圖7.2.1, AB-O-CD區(即雙喇叭區)為反態物質區,是高能態區,能量為負值,空間曲率為負值,滿足羅氏幾何性質;AB- FE-CD區(即球外表面)是正態物質態區,它相對於虛態區為低能...
