歐金尼奧·貝爾特拉米

貝爾特拉米（Eugenio Beltrami，1835年11月16日——1899年6月4日？），義大利數學家，比薩大學教授（1863年）、博洛尼亞大學教授（1866年）、羅馬大學教授（1873年）、帕維西大學教授（1876年）。

貝爾特拉米研究了非歐幾里德幾何學，開拓了超空間的幾何學，還對彈性學的發展作出了貢獻。

基本介紹

• 中文名：貝爾特拉米
• 外文名：Eugenio Beltrami
• 國籍：義大利
• 出生日期：1835年11月16日
• 逝世日期：1899年6月4日，一作1900年2月18日
• 代表作品：Opera matern-atiche（4卷，1902-1920）

主要成就

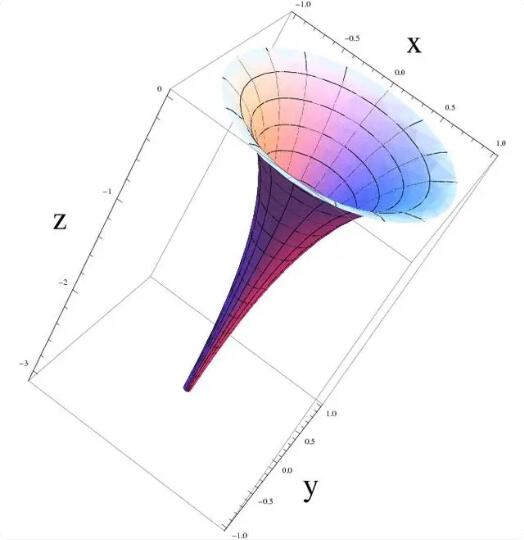
1868年，貝爾特拉米利用當時微分幾何的最新研究成果，發表了一篇著名論文《關於非歐幾里得幾何的解釋》（義大利語：Saggio di inter pretarione della geometria non-euclidea），證明了非歐幾里得幾何（義大利語：geometria non-euclidea）可以在歐幾里德空間中的“偽球面（pseudo-sphere）”，即“曳物線（tractrix）”的“迴轉曲面”上一一對應的實現，從而奠定了羅巴切夫斯基思想得到普遍承認的基礎。

偽球面是一種形如喇叭的特殊曲面，其高斯曲率為負常數的特殊曲面。偽球面的內蘊幾何與羅氏幾何是一致的，一個偽球面可以解釋成為羅氏幾何中一個平面的一部分。這就為羅氏幾何提供了一個模型。

偽球面

這就是說，非歐幾里得幾何命題可以“翻譯”成相應的歐幾里得幾何命題，如果歐幾里得幾何沒有矛盾，非歐幾里得幾何也就自然沒有矛盾。

此後非歐幾里得幾何學的基本思想才開始為人們所理解和接受。

後世影響

因為貝爾特拉米《關於非歐幾里得幾何的解釋》的出現，才將羅巴切夫斯基從非議中解救出來，他所創立的非歐幾里得幾何學的基本思想才開始為人們所理解和接受。

長期無人問津的非歐幾里得幾何開始獲得學術界的普遍注意和深入研究，羅巴切夫斯基的獨創性研究也就由此得到學術界的高度評價和一致讚美，他被人們讚譽為“幾何學中的哥白尼”。

從貝爾特拉米的證明開始，非歐幾里得幾何終於從一個無聊的“牛角尖”，變成了公認的理論。這些鑽牛角尖的人，終於可以揚眉吐氣，證明他們的牛角尖鑽得是有意義的，而且是有很重大的意義的！

稍後，龐加萊和克萊因在歐氏系統也分別構造了羅氏幾何的模型。

龐加萊的模型是：在歐氏平面上劃一條直線而使之分為上、下兩個半平面，把不包括這條直線在內的上半平面作為羅氏平面，其上的歐氏點當做羅氏幾何的點，把以該直線上任一點為中心，任意長為半徑所作出之半圓周算做是羅氏幾何的直線。然後，對如此規定了的羅氏幾何元素一一驗證羅氏幾何諸公理全部成立。

藉助龐加萊模型可以證明羅氏幾何的相對相容性。這種解釋性模型是數理邏輯和數學基礎中的理論研究的重要方法。而描述性數學模型是解決實際套用問題的重要手段。

至此，非歐幾里得幾何才真正獲得了廣泛的理解。