龐加萊模型(Poincare's model)一種羅氏幾何模型。第一個在歐幾里得幾何系統中構造出羅巴切夫斯基幾何公理系統模型的是法國數學家龐加萊(Poincaré,(J.-)H.),由於該模型與非歐幾何的相容性問題以及如何解決第五公設問題等直接相關,從而以龐加萊模型稱之。
基本介紹
- 中文名:龐加萊模型
- 外文名:Poincar's mode
- 模型:羅氏幾何模型
- 構建人物:龐加萊
- 人物簡介:法國數學家
- 空間陳述:5條結合公理I、一I
概念
詳細構造
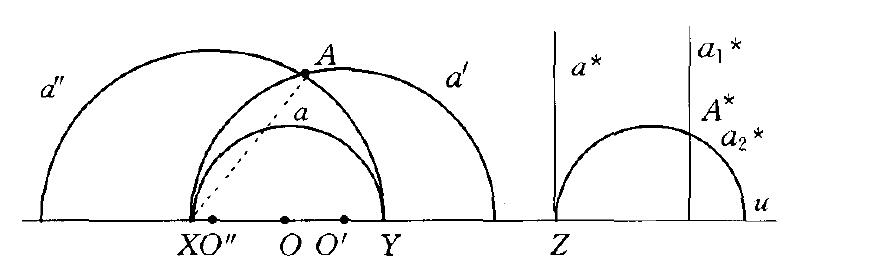 圖1龐加萊模型
圖1龐加萊模型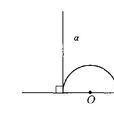
龐加萊模型(Poincare's model)一種羅氏幾何模型。第一個在歐幾里得幾何系統中構造出羅巴切夫斯基幾何公理系統模型的是法國數學家龐加萊(Poincaré,(J.-)H.),由於該模型與非歐幾何的相容性問題以及如何解決第五公設問題等直接相關,從而以龐加萊模型稱之。
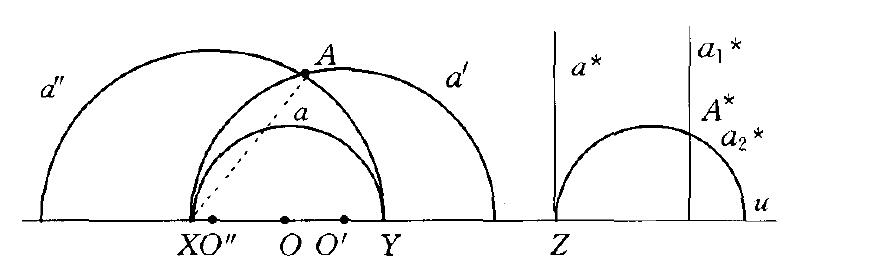 圖1龐加萊模型
圖1龐加萊模型龐加萊模型(Poincare's model)一種羅氏幾何模型。第一個在歐幾里得幾何系統中構造出羅巴切夫斯基幾何公理系統模型的是法國數學家龐加萊(Poincaré,(J.-)H.),由於...
龐加萊複數平面模型(Poincaré complex plane model)是解釋羅氏平面幾何的模型。這個模型是龐加萊((J.-)H.Poincaré)首先提出來的,因為該模型的點是在複數上半...
龐加萊體,均勻流體球自轉時的一種平衡形狀。1885年,龐加萊證明,除馬克勞林橢球體和雅可比橢球體外,均勻流體自轉時還存在另一類平衡形狀。這類平衡形狀與橢球體...
儒勒·昂利·龐加萊(Jules Henri Poincaré,1854—1912年),法國最偉大的數學家之一,理論科學家和科學哲學家。龐加萊被公認是19世紀後和20世紀初的領袖數學家,是...
儒爾斯·亨利·龐加萊,外文名JulesHenriPoincaré,男,法國最偉大的數學家之一,理論科學家和科學哲學家。...
龐加萊一萊特希爾一郭法(Poincare-Lighthill-Kuo method)簡稱PLK法一種偏微分方程數值解法.指用漸近展開法求解非線性數理問題出現高階奇性增強的困難時,把自變數加...
Klein model:在克萊因模型中,“點”仍然是龐加萊圓盤上的點,“直線”是單位圓的所有弦(chord)。這個模型仍然滿足雙曲幾何的所有公理。但克萊因模型中兩條直線的...
在克萊因圓盤模型和龐加萊圓盤模型的雙曲面中,理想點在單位圓(雙曲面)或單位球(較高維度)上,這是雙曲面的不可達邊界。當將相同的雙曲線投射到克萊因圓盤模型和...
的距離。龐加萊度量就是二維雙曲幾何的龐加萊圓盤模型的度量。這定理的要點是把單位圓盤映射到自己的全純函式減少各點間的龐加萊度量下的距離。若上兩不等式有...
是龐加萊度量中兩點<math> z_1,z_2 </math>的距離。 施瓦茨—皮克定理 龐加萊度量就是二維雙曲幾何的龐加萊圓盤模型的度量。這定理的要點是把單位圓盤映射...
36.球極平面投影與保圓變換;雙曲平面的龐加萊模型 …… 拓撲學基本概念數學概覽:直觀幾何編輯推薦 編輯 《數學概覽:直觀幾何(下冊)》是基於一位偉大的數學家...
龐加萊模型和笛卡兒模型的構造成功表明了,在實數系統R無矛盾的前提下,歐幾里得與羅巴切夫斯基幾何公理系統都是無矛盾的(參見“龐加萊模型”、“笛卡兒模型”).因此,...
四、羅巴切夫斯基幾何的模型關於羅巴切夫斯基幾何的困惑歷史上的三個模型交比與分式線性變換龐加萊模型中的非歐距離羅巴切夫斯基幾何的實現...
厄農映射是由法國數學家米歇爾·厄農提出的,以此作為洛倫茨模型的龐加萊截面的簡化模型。對經典厄農映射而言,任意初始點或趨向厄農奇異吸引子,或發散至無窮大。厄農...
第十一章 雙曲幾何的龐加萊模型 第十二章 微積分前期史 第十三章 實數理論 第十四章 極限、連續與積分 第十五章 數學模型 第十六章 外微分形式 第十...
它是關於歐幾里得幾何公理系統是否相容的討論與探索,雖說普遍認為歐幾里得幾何公理系統的相容性是比較信得過的,並對龐加萊模型(即在歐氏幾何系統中構造的羅氏幾何公理...
