基本介紹
- 中文名:絕對幾何
- 外文名:Absolute Geometry
- 提出者:希爾伯特
- 套用學科:幾何學
- 適用領域範圍:數理科學
簡介,結合公理,順序公理,契約公理,連續公理,
簡介
1899年,希爾伯特(D.Hilbert)在他的《幾何基礎》一書中,成功地建立了歐幾里幾何的完整的公理體系,它由五組公理組成,即關聯公理、順序公理、契約公理、連續公理和歐幾里得平行公理。如果去掉歐幾里得平行公理,則以前四組公理為基礎建立起來的幾何稱為絕對幾何。如果用羅巴切夫斯基平行公理取代歐幾里得平行公理,而前四組公理不變,則以此為基礎建立起來的幾何便是羅巴切夫斯基幾何。因此,絕對幾何是歐幾里得幾何和羅巴切夫斯基幾何的公共部分。
結合公理
[axiom of incidence]
結合公理亦稱關聯公理(incidence axioms)或從屬公理(subordinate axiom)。希爾伯特公理系統中規定基本對象“點”,“直線”,“平面”之間結合關係的一組公理。結合關係敘述為“......在......上面”或者“......通過......”,它包括以下八條:
(1)對於任意的兩個點A,B,存在通過這兩點多直線 ;
;

(2)對於任意兩個不同的點A,B,至少存在一條通過它們的直線;
(3)在每一條直線上至少有兩個點:至少存在三個點,不在同一條直線上;
(4)對於不在同一條直線上的三點A、B、C,存在通過每個點點平面 ,在每個平面
,在每個平面 上至少有一個點;
上至少有一個點;


(5)對於任意三個不在同一直線上的點A,B,C,至多有一個通過每個點點平面 ;
;

(6)如果直線 的兩個點A,B 落在平面
的兩個點A,B 落在平面 上,那么直線
上,那么直線 的任何一個點都在平面
的任何一個點都在平面 上;
上;




(7)如果兩個平面有一個公共點,那么它們至少還有第二個公共點;
(8)至少存在四個點,不在同一個平面上。
上面的(1)~(3)可以稱為平面結合公理,(7)表明空間的維數不大於 3,(8)表明空間的維數不小於 3。
順序公理
[axiom of order]
順序公理亦稱次序公理 [axiom of order],希爾伯特公理系統中建立點的順序關係的一組公理。順序關係敘述為“......在......之間”,它包括以下四條:
(1)若點 B 介於 A 與 C 之間,則A,B,C 是一條直線上的不同三點,且點 B 也介於 C 與點 A 之間;
(2)對於任意兩點A,C,直線 AC 上至少存在一點 B,使點 C 在點A,B之間;
(3)在一條直線上的任意三點中,至多有一點在另兩點之間;
(4)(帕施公理)設A,B,C為不在同一直線上的三點,a是平面 ABC 上的一條直線,但不通過三點A,B,C中的任何一點。如果直線 a 通過線段 AB 上的點,那么它或者通過線段 AC 上的點,或者通過線段 BC 上的點。
契約公理
[axiom of congruence]
契約公理亦稱全等公理(axiom of congruence)。希爾伯特公理系統中確定線段或角的契約關係的一組公理。契約關係敘述為“......契約於......”或“......等於......”。它包括以下五條:
(1)設A,B 為直線a上的兩點, 為直線 a 或另一直線
為直線 a 或另一直線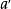 上的一點,則在直線 a 或
上的一點,則在直線 a 或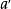 上點
上點 的指定一側,總有一點
的指定一側,總有一點 使線段 AB 契約於線段
使線段 AB 契約於線段 。可用符號記為
。可用符號記為 ;
;

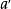
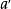




(2)若 ,且
,且 ,則
,則



(3)設 AB 與 BC 為直線 a 上無公共內點的兩個線段,又設 與
與 為同一直線 a 或另一直線
為同一直線 a 或另一直線 上無公共內點的兩個線段,如果
上無公共內點的兩個線段,如果 ,且
,且 ,則必有
,則必有 ;
;






(4)設平面 上有一個角
上有一個角 ,在平面
,在平面 上有一直線
上有一直線 ,而且在平面
,而且在平面 的一側,設
的一側,設 是直線
是直線  上從點
上從點 出發的一條射線,則在平面
出發的一條射線,則在平面 上有且只有一條射線
上有且只有一條射線 。使得
。使得 契約於
契約於 ,且角
,且角 的所有內點均位於
的所有內點均位於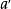 的給定一側,可用符號記為
的給定一側,可用符號記為 。對於任意
。對於任意 ,有
,有 ;
;













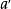



(5)關於 與
與 ,如果有
,如果有 ,
, ,且
,且 ,則必有
,則必有 ,
, 。
。







連續公理
[axiom of continuity]
連續公理是希爾伯特公理系統中確定直線的連續性,並建立線段和角的度量理論的一組公理。它包括以下兩條:
(2)直線完備公理(axiom of linear completeness)一直線上所有滿足結合公理、順序公理、契約公理和阿基米德公理的點的集合不可能擴充成仍然滿足這些公理的更大的集合。直線完備公理等價於康托爾公理。
直線完備公理保證了直線上的一切點可以和實數一一對應起來,它等價於康托爾公理。