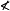羅巴切夫斯基平行公理(Lobachevskian axiom of parallels)是羅巴切夫斯基幾何中最重要的公理，簡稱羅氏平行公理。即存在直線a及不在a上的一點A，過A點至少有兩條直線與a共面且不相交，羅氏平行公理是歐氏平行公理的反面命題。
基本介紹
- 中文名：羅巴切夫斯基平行公理
- 外文名：Lobachevskian axiom of parallels
- 簡稱：羅氏平行公理
- 所屬學科：數學
- 所屬問題：高等幾何(幾何基礎)
公理介紹,相關概念及結論,
公理介紹
公理1 若已知直線L與不在L上的一點P、在L與P確定的平面內，有以P為公共端點且不共線的兩射線PA與PB不與直線L相交，但在這兩射線之間的每一射線都與L相交。
相關概念及結論
定義1. 由公理1保證存在的兩射線PA與PB的每一條叫做過已知點P、從P到A的方向與從P到B的方向平行於已知直線L，並記作PA//L和PB//L。
定義2. 如果一直線它包含過已知點P而平行於已知直線的一射線，就說這直線過P與射線同向平行於已知直線。
定義3. 有兩條射線， 如果第一條射線過已知點而平行於由第二條射線所在的直線，且在由兩射線端點確定的直線的同側，就說這兩條射線在同一方向平行。
定理1. 設P是不在直線L上的一點， 在P點與L確定的平面內，過P且與L相交的射線僅僅是過P平行於L的兩射線之間的射線。
圖1（a）
圖1（b）
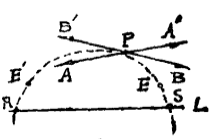圖1（c）證明：如圖1：
設射線PA與PB是過P平行於直線L的兩射線， 要證明只有在PA與PB之間的射線才與L相交，過P的其他射線都與L不相交。
1) PA與PB的反向射線PA'與PB' [如圖1(a)]不與L相交，否則直線PA與直線PB與L相交，這與定義2相矛盾。
2) 在射線PA'與PB'之間的射線與L不相交。 否則如圖1(b)，射線PC'與L交於Q'其反向射線PC與L交於Q，直線CC'與L有公共點Q'和Q，這與公理2相矛盾。
3) 在射線PB'與PA之間的射線不與L相交。否則如圖1(c)，射線PE'與PE都與L相交於R和S，那么射線PA必與L相交，這與假設相矛盾。同理可證在射線PA'與PB之間的射線不與L相交。
於是除PA與PB之間的射線外，過P的射線都不與L相交。
證畢。
從定理1可以看出，直線PA與直線PB把過點P的直線分為兩類，在對頂角∠APB與∠A'PB'之間的直線都與L相交，在對頂角∠APB'與∠BPA'之間的直線都與L不相交，前一類直線叫做對於L的會聚直線，後一類直線叫做對於L的離散直線，加上直線PA與直線PB，過P點在平面內對於L有會聚，離散和平行三種直線存在。
系若PA是過點P平行於直線L的射線，且射線PC與L相交，則射線PA與PC之間的任一射線都與L相交。
定理2.若P是不在直線L上的一點，F是從P到L的垂足，射線PA與PB是過點P平行於L的兩射線，則∠APF=∠BPF。
系若PA是過點P平行於直線L的射線，且射線PC與L相交，則射線PA與PC之間的任一射線都與L相交。
定理2.若P是不在直線L上的一點，F是從P到L的垂足，射線PA與PB是過點P平行於L的兩射線，則∠APF=∠BPF。
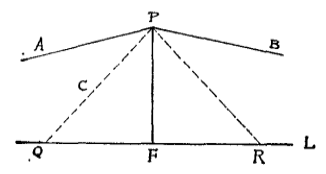圖2證明：若∠APF不契約於∠BPF，則有一角必大於另一角，令∠APF>∠BPF (如圖2)則
1) 在∠APF的內部有一射線PC, 使得∠CPF
∠BPF，因而∠BPF=∠CPF<∠APF。
2) 射線PC是在射線PF與PA之間，必與L交於一點Q。
3) 在射線FQ的反向射線上取一點R，使FRFQ則△PFQ=△PFR (邊、角、邊)
故，∠FPQ≥∠FPR。
4) 但∠FPQ∠FPB,因此∠FPR∠FPB,根據相應公理，射線PR與PB重合。這是不可能的，因為射線PR與L相交， 而射線PB平行於L，所以∠APF
∠BPF，同理∠APF
∠BPF，故得∠APF∠BPF。
系1． 若射線PA與PB是過P點平行於直線L的兩射線，F是從P到L的垂足；則∠APF與∠BPF都是銳角。
(提示：因為∠APB<2直角)
系2． 若射線PA不與直線L相交，但在射線PA與PF(F是L上任一點)之間的任一射線都與L相交，則射線PA過P平行於L。
(提示：反證，設PA不平行於L，則平行於L的另一射線必落在PA么的兩側)
系3． 若點P是不在直線CM上的任一點，過P在直線PC的M一側有唯一射線PA平行於CM。
(提示：反證，設過P還有一射線PA'//CM．則PA'必在PA的兩側。)
系4. 若不共線的兩射線PA與PB，每一條都是過P點平行於同一直線L，則∠APB的平分線垂直於L。
(提示:反證，設角平分線不垂直於L，則∠APB有兩條不同的角平分線。)
系5. 若射線PA//L與射線P'A'//L'，PF與P'F'分別是從P與P'到L與L'的距離，且PF=P'F，則∠APF =∠A'P'F'。
(提示: 反證，設∠APF
∠A'P'F'，則∠APF∠A'P'F'又∠APFA'P'F'。)
從定理2和它的系可以看出：
過已知點對於已知直線有右平行射線或直線，以及有左平行射線或直線。平行公理1指出， 過已知點對於已知直線有唯一的右平行射線或者有唯一的左平行射線。
定義4. 若射線PA//L，F是從P到L的垂足，銳角∠APF叫做對於距離PF=d的平行角。距離PF叫做對於銳角∠APF的平行距。 由定理2知，平行距相同的兩平行角契約。
定理3.一 條直線過一已知點，在一已知方向平行於一已知直線，則過這直線上的每一點在已知方向平行於已知直線。
定理4. 若直線AB平行於直線CD，且點B、D在直線AC的同側，則直線CD平行於AB。
定理5.若直線AB//CD,CD//EF,則AB//EF。
定義6. 有三直線AB, CD和EF.若AB//CD// EF,就說它們在同一方向平行。
定理6. 有兩條平行直線被另一直線所截，同位角不契約。
系1. 兩條平行直線被另一直線所截，則內錯角不契約。
系2. 兩條平行直線被另一直線所截，在同一平行方向的一側，同旁內角和小於2直角。
系3. 兩條直線被另一直線所截，如果有一雙同位角契約，或一雙內錯角契約，或一雙同旁內角互補，那么這兩條直線既不相交也不平行(離散直線)。
定理7. 若a, b, c是三條直線，它們在同一方向平行，且b在a,c之間， 若從b上一點到a與c的垂直線段契約，則從b上任一點到a與c的垂直線段契約。
