貝爾特拉米映射是球面到平面的一種特殊映射。這個映射是貝爾特拉米 (Beltraim,E.)在研究羅氏幾何時首先提出來的,稱為貝爾特拉米映射。
基本介紹
- 中文名:貝爾特拉米映射
- 外文名:Beltrami mapping
- 適用範圍:數理科學
- 提出者:貝爾特拉米
簡介
羅氏幾何的基本性質





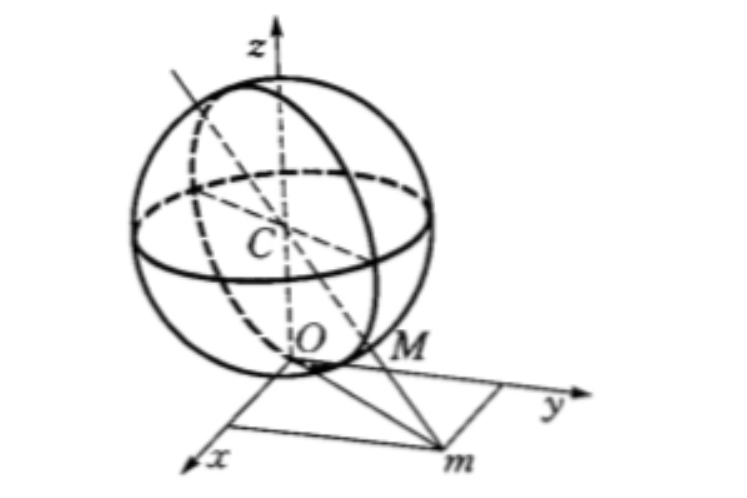
貝爾特拉米映射是球面到平面的一種特殊映射。這個映射是貝爾特拉米 (Beltraim,E.)在研究羅氏幾何時首先提出來的,稱為貝爾特拉米映射。





貝爾特拉米映射是球面到平面的一種特殊映射。這個映射是貝爾特拉米 (Beltraim,E.)在研究羅氏幾何時首先提出來的,稱為貝爾特拉米映射。簡介貝爾特拉米映射是球面到平面的一種特殊映射。在空間直角坐標系中,取一個半徑為 ...
拉普拉斯 - 貝爾特拉米運算元在流形上的本徵函式用作嵌入維數,因為在溫和條件下,該運算元具有可計數的譜,該譜是流形上的平方可積函式的基礎(與單位圓流形上的傅立葉級數相比)。試圖將拉普拉斯特徵映射置於堅實的理論基礎上已經取得了一些成功,因為在某些非限制性假設下,隨著點數變為無窮大,圖拉普拉斯矩陣已經顯示收斂...
- 擬共形映射。這是K-擬共形映射的幾何定義。因為極值長度是不受維數限制的,所以幾何定義可以進行形式推廣而形成高維擬共形映射。這方面的工作只初具規模。當K=1即k=0時,貝爾特拉米方程退化為柯西-黎曼方程;而式(2)則意味著極值長度乃是共形映射下的不變數。1-擬共形映射恰好是共形映射。設ƒ(z)是把|z|...
在一個未知函式的情形,m階線性的偏微分運算元是M上C∞函式的集合C∞(M)到C∞(M)的一個線性映射l,而在每一坐標區域中,l可表示為這裡顯然,在兩個坐標區域的重迭部分,l的兩種表示可以通過坐標變換互相轉換。例如,黎曼流形上的第二類貝爾特拉米運算元,在每一個坐標區域中可表示為這裡gij(x)是度量張量的反變...
其中 是關於度規 的拉普拉斯運算元),則 其中 是 關於 的梯度。博赫納使用這一公式來證明博赫納消沒定理。博赫納恆等式 設M和N為黎曼流形,並令u:M→N為一個調和映射。 設du表示的u的(向前)導數,∇為梯度,Δ為拉普拉斯–貝爾特拉米運算元,RiemN為N上的黎曼曲率張量,RicM為M上的里奇曲率張量,則有 ...
在微分幾何中,博赫納恆等式是關於黎曼流形之間調和映射的恆等式。 它以美國數學家所羅門·博赫納的名字命名。數學表述 設M和N為黎曼流形,並令u:M→N為一個調和映射。 設du表示的u的(向前)導數,∇為梯度,Δ為拉普拉斯–貝爾特拉米運算元,Riem為N上的黎曼曲率張量,Ric為M上的里奇曲率張量,則有 博赫納公式...
拉普拉斯運算元(Laplace Operator)是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,稱為拉普拉斯-貝爾特拉米運算元。定義 拉普拉斯運算元是n維歐幾里德空間中的一個二階微分運算元,定義為梯度(▽f)的散度(▽·f)。因此如果f是二階...
他證明了非對稱齊性西格爾域的形式泊松核不是泊松核,接著提出了如何在非對稱齊性西格爾域上建立調和函式論,即研究拉普拉斯—貝爾特拉米(Laplace-Beltrami)方程的解空間的性質這樣一個重要問題。另一方面,他給出了全純自同構群的李代數的一組標準基及其乘法表,從而提供了研究這類李代數的良好條件。許以超的工作,...
經19世紀60年代貝爾特拉米等人的介紹與推進,黎曼的理論才開始為廣大數學家領悟,他們對微分不變數的研究,最後導致里奇創立張量理論(1887)。在另一篇論文中,黎曼探討了將積分概念推廣到間斷函式上去,提出了現稱為黎曼積分的概念。他構造了具有無窮間斷點而按他的定義仍可積的函式。尋找這類函式是19世紀70~80年代很...
拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元,稱為拉普拉斯-貝爾特拉米運算元。達朗貝爾運算元則推廣為偽黎曼流形上的雙曲型運算元。拉普拉斯–貝爾特拉米運算元還可以推廣為運行於張量場上的運算元(也稱為拉普拉斯–貝爾特拉米運算元)。另外一種把拉普拉斯運算元推廣到偽黎曼流形的方法,是通過拉普拉斯–德拉姆運算元,它作用在微分...
第4章 曲面映射:度量 34 4.1 引言 34 4.2 球面的投影地圖 36 4.3 一般曲面上的度量 38 4.4 度量曲率公式 41 4.5 共形地圖 43 4.6 講一點兒可視化的複分析 45 4.7 球面的共形球極地圖 49 4.8 球極平面投影公式 53 4.9 球極平面投影的保圓性 55 第5章 偽球面和雙曲平面 57 5.1...
6.2.3 球面上的一個共形映射 249 6.2.4 空間旋轉也是默比烏斯變換 252 6.2.5 空間旋轉與四元數 256 6.3 雙曲幾何 259 6.3.1 曳物線和偽球面 259 6.3.2 偽球面的常值負曲率 260 6.3.3 偽球面上的一個共形映射 261 6.3.4 貝爾特拉米的雙曲平面 263 6.3.5 雙曲直線和反射 266 6.3.6...
§2曲線類和區域類·保角映射的某些性質//12 §3柯西型積分的某些性質//14 §4非齊次柯西一黎曼方程組//16 §5在索伯列夫意義下的廣義微商和它們的性質//19 §6運算元Tf的性質//26 §7函式類D1.的格林公式·面積微商//37 §8Tcf型函式的微分性質·運算元Ⅱf//39 §9運算元Ⅱf的擴充//46 §10D(G)與...
3.1.3 拓撲空間的映射 71 3.1.4 拓撲不變性 72 3.2 微分流形 74 3.2.1 拓撲流形 74 3.2.2 微分流形 75 3.2.3 微分流形的例子 76 附錄3.2 黎曼生平及學術貢獻 79 3.3 光滑映射和微分同胚 81 3.3.1 流形間的光滑映射 81 3.3.2 微分同胚 82 附錄3.3 惠...
