流形邊界(boundary of manifold)是一個數學名詞，指帶邊流形中全體邊界點的集合。
基本介紹
- 中文名：流形邊界
- 屬性：數學名詞
設M是n維帶邊流形，p是M的圖冊.對於pEM，若存在卡(p＞E)，使得p ＞ R+，其中稱p為M的邊界點(見圖).p是M的邊界點與卡(Ua,p)的選取無關.M的全體邊界點的集合稱為的邊界，它是(n-1)維的(無邊)流形，記為aM,pE M- aM稱為M的內點，M- aM是n維(無邊)流形.
流形邊界
流形邊界(boundary of manifold)是一個數學名詞，指帶邊流形中全體邊界點的集合。
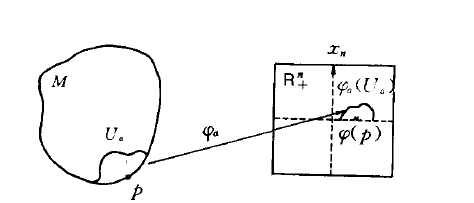
流形邊界(boundary of manifold)是一個數學名詞，指帶邊流形中全體邊界點的集合。設M是n維帶邊流形，p是M的圖冊.對於pEM，若存在卡(p＞E)，使得p ＞ R+，其中稱p為M的邊界點(見圖).p是M的...
帶邊流形(manifold with boundary)是一類特殊的拓撲流形。它具有可數基和T2分離性，並且局部同胚於歐氏空間中半空間的拓撲空間。定義 n維帶邊拓撲流形是第二可數空間和豪斯多夫空間M，且M上每點均存在鄰域拓撲等價於 或 的開集。性質 設M為帶邊拓撲流形。M為局部緊空間。M為仿緊空間。M為局部道路連通空間。M的...
流形協邊 [1](cobordism of manifolds)微分拓撲學的一個重要概念中文名 流形協邊 外文名 cobordism of manifolds 流形協邊 [1](cobordism of manifolds)微分拓撲學的一個重要概念.兩個流形的互不相交的並恰是某個流形的邊界.設M M:都是緊緻(無邊)微分流形,若存在緊緻帶邊流形W與微分同胚aW-MU Mz,則稱為...
流形定義 設M為帶邊流形，則p∈M稱為M的流形邊界點，若存在坐標卡(U,φ)，使得φ(p)為 中的邊界點。舉例 例1 設A=[-1，0）∪{1/n | n∈N}，則 例2 考慮有理點集Q，則 拓展 邊界點處理在數據挖掘技術中有重要意義，它們代表了一類歸屬並不明確的個體，如果單純地依靠某種方法把其歸類到一個特定...
帶邊C流形（Ck manifold with boundry）是一種有邊緣的C類微分流形。簡介 帶邊C流形是一種有邊緣的C類微分流形。設M是一個仿緊豪斯多夫空間，{(U,𝜙)|i∈I}是一個圖冊，其中U是M中的開集，𝜙是U到 的一個開集上的同胚，使得當U∩U≠∅時，映射 是C類的，且至少有一個U，使得𝜙(U)∩R≠...
《關於帶邊流形上的k-Yamabe問題的研究》是依託中南大學，由賀妍擔任項目負責人的青年科學基金項目。項目摘要 本項目將深入研究帶邊流形上的k-Yamabe問題。該問題是微分幾何中的一個熱點，在本質上就是要解一個Neumann邊值條件的完全非線性的偏微分方程。本項目將立足於已有的前期工作，將帶邊流形上的k-Yamabe問題...
§24.流形的邊界 §25.流形上標量函式的積分 第六章 微分形式 §26.多重線性代數 §27.交錯張量 §28.楔積 §29.切向量和微分形式 §30.微分運算元 §31.對向量場和標量場的套用 §32.可微映射的作用 第七章 Stokes定理 §33.參數流形上的形式的積分 §34.可定向流形 §35.定向流形上形式的積分 §36....
定義 設M是帶邊的定向流形，是給出M定向的圖冊。的定向由圖冊 給出的 的定向稱為與M的定向是協調的。引理1 同胚於圓盤與Mf；bius帶沿公共邊界的粘合。引理2Klein 瓶同胚於粘合了兩個 帶的球面。定理2(分類定理)任何光滑、緊緻、連通、閉、二維流形或同胚於有k 個柄的球面 ，或同胚於有s 個 膜的球面 。...
這門學科的主要任務，首先是闡明流形的拓撲結構和組合結構，同時如同拓撲學把研究連續映射作為重要問題之一，微分拓撲學也把研究可微映射作為重要的課題。它研究的中心問題如下面所列：微分同胚問題： 判斷兩個微分流形是否微分同胚。配邊問題： 給一個光滑緊緻無邊的微分流形，判斷它是否為某帶邊微分流形的邊界。微分...
《典型流形與典型域》是2011年科學出版社出版的圖書，作者是陸啟鏗。內容簡介 《典型流形與典型域》是我國數學家在多復變數函式論研究中關於幾何理論方面創作的系統總結．內容包括典型流形、超圓與典型域、橢圓幾何與雙曲幾何、解析不變數及其套用、對稱典型域的邊界之幾何性質及其套用、典型域的調和函式論等六章，另...
13.2.1 雙曲3-流形與球3-流形 181 13.2.2 幾何化定理 184 習題 185 第14章 三維流形拓撲中的一些決定問題 186 14.1 兩個預備引理 186 14.2 套用1：分裂鏈環的決定 188 14.3 套用2：找本質球面 189 14.4 套用3：判定3-流形邊界的可壓縮性和紐結的平凡性 193 習題 197 第15章 ...
我們將主要從CR幾何的角度研究負曲率完備凱勒流形的邊界，研究容許負常數截面曲率上界的完備凱勒度量的有界區域到復單位球中的常態全純嵌入的存在性、雙圓盤上甚至有界偽凸區域上具有負常數截面曲率上界的凱勒度量的完備點以及通過幾何熱流進一步解決伍鴻熙和鄭方陽教授的分解猜想。結題摘要 在項目執行期間，我們主要研究了...
本項目主要研究帶邊三維流形沿邊界上子曲面融合後，Heegaard虧格非退化的條件以及退化的下界。內容包括：研究Hempel的Heegaard距離概念的推廣，使之能夠包含流形和分解的更多拓撲和幾何信息，從而能更好的反映流形及分解的性質，並利用所得的性質研究3-流形（及其Heegaard分解）在一定條件下融合時的虧格變化範圍。研究的結果...
每個黎曼曲面都是二維實解析流形(也就是曲面)，但它有更多的結構(特別是一個復結構)，因為多值函式的無歧義的定義需要用到這些結構。一個實二維流形可以變成為一個黎曼曲面(通常有幾種不同的方式)若且唯若它是可定向的。所以球和環有復結構，但是莫比烏斯圈，克萊因瓶和投影平面沒有。詳細說明 單值解析函式的反...
歐幾里得空間中子流形是極小的，若且唯若其坐標函式是該子流形上的調和函式。具有非正截面曲率的完備單連通黎曼流形中不存在閉的極小子流形。幾何意義 極小子流形的幾何意義是: 設 是浸入在黎曼流形 中的子流形。如果每一點 都有一個開鄰域 U，使得 是緊緻的,並且對於 的任意一個有固定邊界的變分 ...
本項目擬在前期工作的基礎上開展以下方面的研究： (1)由於一致穩定性是Toric流形上的極值Kahler度量存在的必要條件,我們希望得到在一致穩定性的條件下高維Toric流形的各個余維數的邊界附近鄰域的正則性。這是證明光滑的極值Kahler度量存在性的關鍵一步。 (2)首先利用Calabi流來研究Toric曲面上的極值度量，考慮Calabi流在...
1.兩個微分流形在什麼條件下是微分同胚的?2.若兩個微分流形是同胚的，則它們一定微分同胚嗎?3.一個微分流形能嵌入或浸入到另一個微分流形中嗎?4.怎樣的微分流形是另一個帶邊流形的邊界?5.一個微分流形是否可平行化.19世紀末，龐加萊(Poincaré，(J.-)H.)在代數拓撲學方面做了一系列奠基工作的同時，對3維...
研究了具有負Ricci曲率下界的緊緻帶邊流形， 在邊界的平均曲率為嚴格正下界的假定下， 給出直徑的最優上界估計。 (5) Weyl共形泛函的研究：研究了黎曼流形上一類共性不變泛函（Weyl 泛函）的變分問題，計算了Weyl 泛函的第一，第二變分，並證明兩個3維單位球面乘積是Weyl 泛函的嚴格穩定點（即第二變分為正）。
通過對不可壓縮、邊界不可壓縮曲面性質的研究，從而討論幾乎交錯紐結的Cabling猜想；研究不可壓縮、分段不可壓縮曲面的歐拉示性數以及虧格等問題.同時研究紐結不變數，特別是有限型不變數以及它們的微分性質，從而研究三維流形的不變數的性質.預期的結果將揭示3、4-維流形的許多內在的拓撲性質.
《三維流形上的Dehn手術及把柄添加》是依託吉林大學，由邱瑞鋒擔任項目負責人的青年科學基金項目。項目摘要 本項目擬研究3－流形上的Dehn手術及把柄添加，重點研究3－流形的約化性、邊界薊院退緣戎匾災試?Dehn手術及把柄添加實施過程中的穩定性，這是3－流形理論的重要課題之一。展開本項目的研究對於全面...
三是研究了Minkowski空間中具有毛細邊界的類空圖超曲面的平均曲率流問題，證明了該流具有長時間存在性並收斂到平移解。（2）黎曼流形上橢圓運算元的特徵值估計方面，我們一是給出了Heisenberg群上有界區域水平切叢上橢圓運算元的特徵值估計，二是研究了緊緻流形或子流形上四階散度型加權橢圓運算元和雙Drifting拉譜拉斯運算元的...
這些問題包括奇點領域擬凸CR流形邊界的等價分類問題， CR流形形變問題和復Plateau問題等。 我們研究的這些問題涵蓋了代數幾何，復幾何和微分幾何等領域， 目前在奇點理論和CR幾何的研究中占有重要地位。結題摘要 本項目主要取得了三個方面的成果： 1. 奇點不變數：解決了Yau關於Griffiths數的不等式猜想； 2. CR幾何...
他們計畫研究相應的Frobenius流形結構，DGBV代數結構，B模型的CY/LG對應，高虧格的B理論以及與GW理論，FJRW理論之間的關係。進一步的研究還將擴展到開弦的研究。這些問題的解決將使人們更進一步的理解二維拓撲場理論和鏡像對稱。除此之外，申請人還將研究非正曲率CH流形邊界的緊化問題。這個項目的開展也將有助於我國...
龐加萊猜想是一個拓撲學中帶有基本意義的命題，將有助於人類更好地研究三維空間，其帶來的結果將會加深人們對流形性質的認識。陳述 1904年，法國數學家亨利·龐加萊提出了一個拓撲學的猜想：“任何一個單連通的，閉的三維流形一定同胚於一個三維的球面。”簡單的說，一個閉的三維流形就是一個有邊界的三維空間；...
是自由部分與整數係數有關的流形。然後是雙線性映射，即對偶性配對。和 第一種形式通常稱為交叉形式，第二種是扭轉聯接形式。 假設流形M是平滑的，則通過擾動流形類別來橫向計算交叉乘積並計算它們的定向交叉數。 對於扭轉連結形式，通過實現nx作為某個類z的邊界來計算x和y的配對。 形式是分子的分數，z的橫向交叉...
閉曲面是指沒有邊界點的緊緻連通2維實流形（曲面）。它分為可定向曲面與不可定向曲面。封閉的表面是緊湊且沒有邊界的表面。 示例是像球體，環面和克萊恩瓶子這樣的空間。非封閉表面的示例是：開放盤，其是具有穿刺的球體；圓柱體，是具有兩個穿刺的球體；和莫比斯（Möbius）地帶。 與任何封閉的歧管一樣，嵌入...
具體說來，由范卡彭定理易知有下列結果：若M為有g個奇異纖維的賽費特纖維空間，其賽費特曲面S有虧格g以及k個邊界分支。若賽費特纖維空間M為閉流形，則其中的賽費特結構可能不惟一，但是它上面的齊性幾何由兩個不變數決定，其一為賽費特曲面S的歐拉示性數χ，其二為M的歐拉示性數e。3維流形的幾何 研究3維流形...
設M是一個緊的二維黎曼流形， 是其邊界。令K為M的高斯曲率， 為 的測地曲率。則有 其中dA是該曲面的面積元，ds是M邊界的線元。此處 是 的歐拉示性數。如果 的邊界是分段光滑的，我們將 視作光滑部分相應的積分之和，加上光滑部分在曲線邊界上的轉過的角度之和。一般化的高斯-博內定理 廣義高斯-...
體積元(volume element)是一種外微分形式，微分流形上與定向相符的外微分形式。更一般地，一個體積元是流形上一個測度。簡介 數學中，體積元提供了函式在不同坐標系（比如球坐標和圓柱坐標）下對體積積分的一種工具。更一般地，一個體積元是流形上一個測度。在一個定向 -維流形上，體積元典型地由體積形式生成...
素分解存在惟一性定理 [1](the existence anduniqueness theorem for prime decomposition)是幾何拓撲學的一個重要定理。中文名 素分解存在惟一性定理 外文名 the existence anduniqueness theorem for prime decomposition 簡介 3維流形分解為素3維流形的連通和的可能性以及這種分解的惟一性問題.對於一個無Sz邊界的3維...