基本介紹
- 中文名:可定向流形
- 外文名:orientable manifold
- 所屬學科:數學
- 所屬領域:幾何拓撲學
- 釋義:確定流形指向的方式問題
基本介紹


























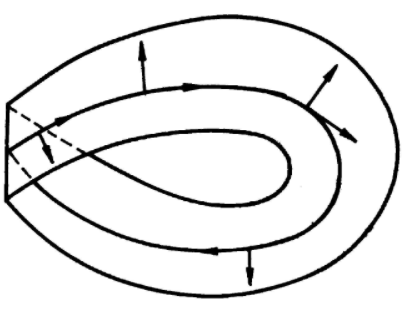
相關性質定理






















































































流形M的定向就是其連續逐點定向。性質 每個李群都是可定向流形。當n>1時,n維球面是可定向流形。實射影空間ℝPⁿ為可定向流形,若且唯若n是奇數。R定向 定義 n維流形M的R定向為開覆蓋{U}與M在U的R基本同調類z,滿足若U⋂...
對於不可定向流形,相當於球面定理的有衣潑斯坦(Epstein,D.B.A)的射影平面定理。其大意是說,若M為任意3維流形,π2(M)≠0,則存在連續映射g:S²→M,使得g:S²→g(S²)或者為同胚,或者為2倍覆疊,而g不同倫於0...
為緊連通可定向流形。概念 復射影空間是實射影空間的推廣,即復歐幾里得空間添加無窮遠點構成的空間。添加了無窮遠點的複平面稱為一維復射影空間,記為 ,推廣到n維,便得到n維復射影空間,其具體構作如下:給定n+1維復歐氏空間C,考慮...
流形的定向類似於數學分析中給曲面確定方向那樣給流形確定方向。設M是n維連通微分流形,若M是可定向流形,Λⁿ(M*)\O的兩個分支之一的一種選擇稱為流形M的定向。若M是可定向的非連通流形,則M的定向是M的每個分支上定向的一個...
§34.可定向流形 §35.定向流形上形式的積分 §36.形式和積分的幾何解釋 §37.廣義Stokes定理 §38.對向量分析的套用 第八章 閉形式和恰當形式 §39.Poincaré引理 §40.有孔Euclid空間的de Rham群 第九章 尾聲——Rn之外的世界 ...
S')隨S(或s')的改變定向而改變符號,所以決定一個對稱雙線性形式或相交形式由龐加萊對偶定理可知, xr為交換群HZ (M; Z)的一個基,則行列式一個經典的結果是,可由f決定M的同倫型,即,懷特海定理:兩個緊緻單連通的4維流形是...
定向配邊類(oriented cobordism class)是流形的一種等價類,對於兩個光滑緊定向n維流形M與M′,若存在一個光滑緊的帶邊的定向流形X,使得∂X及其誘導定向在保持定向的同胚之下同胚於M與(-M′)的無交並,則稱M與M′屬於同一個...
總是保向同胚,則稱M為可定向流形;否則,稱為不可定向流形。設 為單位區間, 為流形M的一條道路,選取 的一個分割 使得 某 ,現在通過 選取 的序向,使得在 和 上,它們有一致的序向,則當a為環道時,有a(0...
不可定向流形 不可定向流形(non-orientable manifold)是1993年發布的數學名詞。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
k=ω時,是解析流形。C流形又常稱為光滑流形。如果微分流形M是一個仿緊或緊空間,則稱M為仿緊或緊微分流形。如果可選取坐標圖冊使微分流形M中各個坐標鄰域之間的坐標變換的雅可比行列式都大於零,則稱這個流形是可定向的。球面是可定向...
流形上微分運算元理論是流形上的分析的一個分支,它研究流形上橢圓微分運算元及擬微分運算元的阿蒂亞-辛格指標定理及其套用。線性微分運算元 設M是緊可定向流形,E,F是M上的C復向量叢,線性映射P:C(E)→C(F),其中C(E)與C(F)分別是E...
不可壓縮曲面在3維流形的研究中起著重要的作用.有如下定理:若M為緊緻3維流形,}M中的每個分支在M中不可壓縮,群的自由積,則關於不可定向流形,衣潑斯坦((Epstein,D. B. A.)也有一個重要的定理:設M為不可定向3維流形,若它...
n)×1,這裡U(n)是酉群。因此,每個切觸流形是可定向的。歐氏空間R中的單位球面S和n+1維黎曼流形的切球叢是簡單的典型例子,二者都具有自然的切觸形式。每個3維緊的可定向微分流形均為切觸流形。
流形可定向若且唯若其切叢可定向。流形為自旋流形,若且唯若其切叢有自旋結構。流形M₁與M₂的積流形M₁×M₂的斯蒂弗爾-惠特尼多項式為w(t)=w(t)w(t),其中w(t)與w(t)分別為M₁與M₂的斯蒂弗爾-惠特尼多項式。若...
2. 所有臨界元素是雙曲的;3. 無鞍點間的連線軌道。定理3 (Peixoto)設M為緊緻 二維可定向流形(),若且唯若 是M-S向量場時,為結構穩定。定理4 (帕利斯-斯梅爾)每一微分同胚 是 結構穩定的,每一個向量場 是 結構穩定的。
1 可定向流形 2 定向映射度與定向環繞數 3 hopf定理 練習i 第十章 局部映射度, leray乘積公式與jordan-brouwer 分離定理 1 映射度定義的局部化 2 leray乘積公式 3 jordan-brouwer分離定理 4 緊緻超曲面的分離性質 練習j 第十一章 ...
上述協邊理論有很多推廣,如可定向流形的協邊論,映射的協邊論,穩定切叢有復結構的流形的協邊論,穩定切叢有標架的流形的協邊論等等。其中標架協邊論與球的同倫群的研究有著互逆的關係,仍是拓撲學中重要的難題。微分拓撲雖是不同...
在只定義在單純復形的單純同調之上,還可以使用光滑流形的微分結構來通過德拉姆上同調或Čech上同調或層上同調來研究定義在流形上的微分方程的可解性。德拉姆證明所有這些方法是相互關聯的,並且對於閉可定向流形,通過單純同調得出的貝蒂...
這是說貝蒂數:閉合(即緊湊且無邊界)可定向的n流形的第k和(n-k)貝蒂數相等。在那個時候,上同調的概念被澄清了大約40年。在他1895年的論文分析中,龐加萊試圖用他發明的拓撲交叉理論來證明這個定理。對他的作品的批評使他意識...
4.5.1 帶邊流形 4.5.2 可定向流形 4.5.3 二維流形的分類 4.6 作為二維流形的代數函式的黎曼曲面 第五章 張量分析與黎曼幾何 5.1 流形上張量場的一般概念 5.2 張量場的簡單例子 5.2.1 例 5.2.2 張量的代數...
3.1.5黎曼流形 3.2微分形式 3.2.1格拉斯曼代數 3.2.2微分形式 3.2.3外微分 3.2.4龐卡萊引理及逆命題 3.2.5對偶映射 3.3流形上的積分 3.3.1體形式與可定向流形 3.3.2流形上的積分 3.3.3斯托克斯定理 3.4臨界點...
本書是一本入門性的現代數學教材,簡要介紹與科學技術密切相關的一些重要現代數學分支的基本概念、方法和套用,為進一步深入學習和套用現代數學知識打下基礎。它主要包括近世代數與拓撲、非線性泛函分析、微分流形及其套用、偏微分方程的現代...
的定理,對於可定向流形這樣的連通和分解除了因子的次序差別以外,在同胚的意義之下,是惟一確定的.對於不可定向流形,設屍為S‘上的不可定向Sa叢,M為不可定向流形,若有M=Mn,則必然還有M=Mb,M的這種改變稱為標準化.上述惟一性定理...
2.漸進酉表示 在幾乎酉表示的基礎之上,V. M. Manuilov進而給出如下漸進酉表示的概念。Γ的任意幾乎酉表示都可以納入到一個漸進酉表示當中去。有限生成群的例子有自由群、有限群、交換群以及二維可定向流形的基本群等。
注意,若M,N不是可定向流形,f:M→N為連續映射,則取與f同倫的C映射h:M→N,對於h的正則值q∈N,記deg₂(h,q)為h(q)M中點的個數的模2剩餘類,它與h,q的選取無關,於是,稱deg₂(f)=deg₂(h,q)為f的模...
注意,當M,N或A不是可定向流形時,可類似於模2映射度而定義模2相交數#₂(f,A)。映射 亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G的定義域D(G)為X,且對任何x∈X都有惟一的y∈Y滿足G(x...
若兩個流形是可定向的,由逆轉定向黏合映射定義的連通和是惟一的。即使這建構使用到的球的選擇,但最後結果都會於同胚下統一。亦可以將此運算作用於光滑範疇上,而其結果也會於微分同胚下統一。連通和的運算標記為#;例如,A#B即表示...
2.任何閉3維流形上,若有模型於上述意義下的幾何,則這種幾何是惟一的。當然,瑟斯頓也注意到在閉3維流形的非平凡連通和之中,除了RP#RP以外,均無上述意義下的幾何,因此他的工作中也包含一些幾何猜想,即他認為任何緊緻、可定向3維...
進一步的,我們希望證明每個單凸多面體所對應的諸多小覆蓋中,都有一個可定向的流形。這樣,我們就可以完全繞開四色定理,給出3維情形環面拓撲的一些基本性質的證明。結題摘要 此項目致力於證明三維單凸多面體的Buchstaber不變論為面數減...
