相關詞條
- 連通和
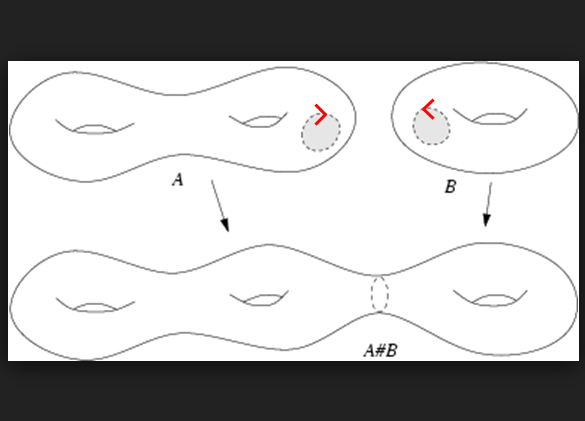
在數學裡,尤其是在拓撲學裡,連通和的運算是指一於流形上的幾何改變。其效果為將兩個給定的流形於各個選定的點附近連線起來。此一建構在閉曲面分類上有著關鍵性的角色。更一般地,也可以將流形和其子流形連線起來;此一廣義化通常稱為纖...
- 弱2k-連通和幾種連通度的研究及有效算法
《弱2k-連通和幾種連通度的研究及有效算法》是依託中山大學,由婁定俊擔任項目負責人的面上項目。中文摘要 連通度是圖的重要性質。本項目根據n-可擴圖的研究進展,引入弱2k-連通圖的局部弱2k -連通圖的概念。本項目的目標是刻劃弱2k...
- 連通(拓撲學概念)
拓撲空間的極大連通子集稱作連通單元,每個空間都能表成它的連通單元的不相交聯集。連通單元必然是閉的,在夠好的空間(如流形、代數簇)上也同時是開的,但並非總是如此。例如有理數集上的連通單元都是單元素集合。如果一個空間的...
- 連通關係
連通關係(connected relation)亦稱弱連通關係、嚴格可比關係,是一種特殊的關係。在類K中,對於一個關係R來說,如果類K中任意兩個不同的個體x,y,至少使二公式:xRy,yRx中有一個為真,則稱關係R在類K中是連通的關係。例如,在...
- 字形和表象有關任務的腦功能連通和性別差異研究
《字形和表象有關任務的腦功能連通和性別差異研究》是2008年於慶寶編寫的論文,由唐一源指導。副題名 外文題名 Study of sex differences and functional connectivity during orthography and imagery tasks 論文作者 於慶寶著 導師 唐一源...
- 2020年5G,連通性和移動性國際研討會
2020年5G,連通性和移動性國際研討會是於2020年10月9-11日線上上舉辦的國際會議。出版和索引 所有接受的論文將線上出版,將被Ei Compendex,SCOPUS,Google Scholar,Cambridge Scientific Abstracts(CSA),Inspec, ISTP等檢索,優秀論文...
- 連通性分析
連通性是指空間或集合的一種拓撲性質。直觀地說,連通就是連成一片沒有間斷。數軸上的區間是連通的。連通性分析是根據指定的起始和終止結點,分析兩點之間是否連通;或根據指定多個點,分析多個點之間是否互通。方法簡介 連通性分析是根據...
- 海南島河湖水系連通與水資源聯合調配研究
《海南島河湖水系連通與水資源聯合調配研究》是2019年中國水利水電出版社出版的圖書。內容簡介 本項目揭示了河湖水系連通概念、及特徵,構建基於系統動力學和集對分析等方法的河湖水系連通評價模型,對河湖水系連通現狀進行分析評價。針對不...
- 連通問題
連通問題 連通問題是一種圖論問題.在可以把問題歸結為建立兩元素間聯繫的數學問題中,思維圖的運算可以歸結為安插新的結點和邊,最終完成包含表示這兩元素結點的一個連通圖。連通問題(connectivity problem)
- 連通區域
複平面上的一個區域G,如果在其中任做一條簡單閉曲線,而閉曲線的內部總屬於G,就稱G為單連通區域。一個區域如果不是單連通區域,就稱為多連通區域。定義 區域:平麵點集D稱為區域,如果它滿足如下兩個條件:(1)D是一個開集;(...
- 連通圖
在圖論中,連通圖基於連通的概念。在一個無向圖 G 中,若從頂點i到頂點j有路徑相連(當然從j到i也一定有路徑),則稱i和j是連通的。如果 G 是有向圖,那么連線i和j的路徑中所有的邊都必須同向。如果圖中任意兩點都是連通的,...
- 連通分量
無向圖G的極大連通子圖稱為G的連通分量( Connected Component)。任何連通圖的連通分量只有一個,即是其自身,非連通的無向圖有多個連通分量。定義 無向圖 的極大連通子圖稱為 的連通分量( Connected Component)。任何連通圖的連通分量...
- 全面預算之美:連通戰略和經營的利器
《全面預算之美:連通戰略和經營的利器》是2017年機械工業出版社出版的圖書,作者是史永翔。目錄 前言 第1章 企業為什麼要做預算 /1 1.1 為什麼要做預算 /3 1.1.1 管理者(老闆)如何看預算 /3 【案例與思考】企業如何...
- 物聯網連通性及系統集成(英漢雙語)
《物聯網連通性及系統集成(英漢雙語)》是中國電力出版社出版的書籍。內容簡介 《物聯網連通性及系統集成(英漢雙語)Connectivity and Integrated Approach for IoT》是一本針對物聯網、智慧型手機和各種嵌入式設備套用開發的實用性技術書...
- 連通器
幾個底部互相連通的容器,注入同一種液體,在液體不流動時連通器內各容器的液面總是保持在同一水平面上。連通器的原理可用液體壓強來解釋。若在U形玻璃管中裝有同一種液體,在連通器的底部正中構想有一個小液片AB。假如液體是靜止不...
- 關於開展2021年水系連通及水美鄉村建設試點的通知
2021年4月7日,水利部規劃計畫司、財政部農業農村司以規計計函〔2021〕16號印發《關於開展2021年水系連通及水美鄉村建設試點的通知》。通知全文 關於開展2021年水系連通及水美鄉村建設試點的通知 (規計計函〔2021〕16號 )有關省、...
- 單向連通圖
的通路,即頂點之間的可達關係沒有對稱性。因此,有向圖的連通性分為強連通、單向連通和弱連通3種。定義1設D是一個有向圖,如果D中任意兩個結點都彼此可達,則稱D為強連通圖。如果D中任意兩點 之間,有 到 可達或 到 可...
- 絲綢之路:連通伊斯坦堡和中國西安的歷史之路
《絲綢之路:連通伊斯坦堡和中國西安的歷史之路》是一本2023年重慶出版社出版的圖書,作者是麗塔·亨斯。內容簡介 本書《絲綢之路:連通伊斯坦堡和中國西安的歷史之路》,是以圖文的方式對絲綢之路西方名城伊斯坦堡至東方古都西安路段...
- 連通分支
設R為空間X中點的連通關係,每個等價類R[x]稱為空間X的一個連通分支。設Y為空間X的非空子集,Y作為X的子空間的連通分支稱為X的子集Y的連通分支。定義 設x,y是空間X中的兩點,如果存在X的連通子集 ,則稱點 是連通的。①...
- 電子設備互連與連線
一部電子設備由若干個甚至幾十萬個電子元件、器件和機電元件組成;這些元件須按電路圖互相連線方能完成預定功能。任何兩個分立接點之間的電氣連通稱為互連;兩個緊連的接點的電氣連通稱為連線。互連繫統應正確可靠,並符合信號傳輸的技術...
- 拓撲學(數學學科)
拓撲學(topology),是研究幾何圖形或空間在連續改變形狀後還能保持不變的一些性質的學科。它只考慮物體間的位置關係而不考慮它們的形狀和大小。在拓撲學裡,重要的拓撲性質包括連通性與緊緻性。拓撲英文名是Topology,直譯是“地誌學”,...