基本介紹
- 中文名:連通分量
- 外文名:connected component
- 所屬領域:圖論、數據結構
- 別稱:極大連通子圖
- 相關概念:無向圖、強連通分量等
定義
相關概念
路徑
頂點間的連通性
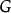
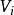
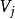
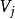
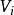
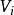
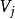
連通圖
強連通圖
強連通分量
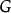
求無向圖的連通分量


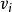
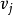
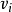
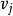

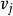

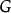
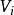
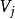
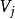
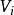
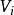
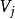


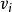
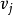
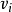
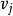

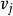
無向圖G的極大連通子圖稱為G的連通分量( Connected Component)。任何連通圖的連通分量只有一個,即是其自身,非連通的無向圖有多個連通分量。...
有向圖強連通分量:在有向圖G中,如果兩個頂點vi,vj間(vi>vj)有一條從vi到vj的有向路徑,同時還有一條從vj到vi的有向路徑,則稱兩個頂點強連通(strongly ...
雙連通分量有點雙連通分量和邊雙連通分量兩種。若一個無向圖中的去掉任意一個節點(一條邊)都不會改變此圖的連通性,即不存在割點(橋),則稱作點(邊)雙連通圖...
連通分量標定 (Connected Component Labeling)是圖論中的一個算法,它會給連通的象素點一個唯一的標號。計算機視覺中的連通分量標定通常用來處理二值圖像,但是灰度、...
scc(strongly connected components) 有向圖強連通分量在有向圖G中,如果兩個頂點vi,vj間(vi<>vj)有一條從vi到vj的有向路徑,同時還有一條從vj到vi的有向路徑...
在圖論中,連通圖基於連通的概念。在一個無向圖 G 中,若從頂點i到頂點j有路徑相連(當然從j到i也一定有路徑),則稱i和j是連通的。如果 G 是有向圖,那么...
在圖論中,連通圖基於連通的概念。在一個無向圖G中,若從頂點到頂點有路徑相連(當然從到也一定有路徑),則稱和是連通的。如果G是有向圖,那么連線和的路徑中所有...
強連通圖(Strongly Connected Graph)是指在有向圖G中,如果對於每一對vi、vj,vi≠vj,從vi到vj和從vj到vi都存在路徑,則稱G是強連通圖。有向圖中的極大強...
強連通(Strongly Connected)是指一個有向圖(Directed Graph)中任意兩點v1、v2間存在v1到v2的路徑(path)及v2到v1的路徑。...
關節點是指在某圖中,如果刪除頂點V以及V相關的邊後,圖的一個連通分量分割為兩個或兩個以上的連通分量,則稱頂點V為該圖的一個關節點。...
如果連通無向圖G中存在一個點u,刪除u後G不再連通,則稱u為G的一個割點(articulationpoint) 。沒有割點的連通圖稱為雙連通圖(biconnected graph) 。對於任意兩...
在計算機科學中,Kosaraju的算法(也稱為Kosaraju-Sharir算法)是線性時間的算法來找到一個有向圖的強連通分量。Aho, Hopcroft 和Ullman相信這個算法是由S. Rao ...
一種由Robert Tarjan提出的求解有向圖強連通分量的線性時間的算法。...... Tarjan算法是用來求有向圖的強連通分量的。求有向圖的強連通分量的Tarjan算法是以其發明...
