一種由Robert Tarjan提出的求解有向圖強連通分量的線性時間的算法。
基本介紹
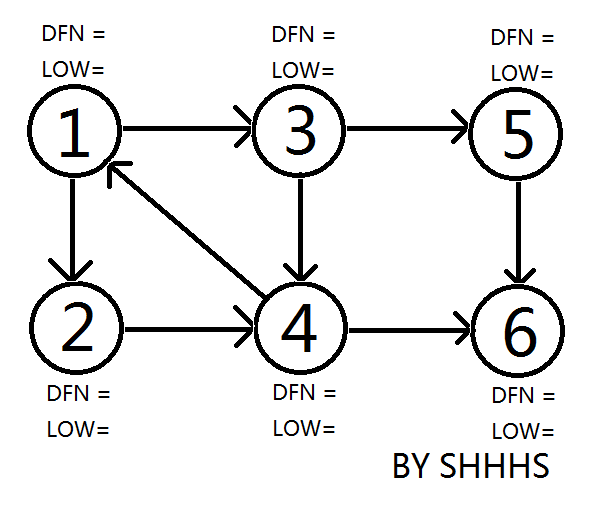
算法介紹




實例代碼
偽代碼
tarjan(u){ DFN[u]=Low[u]=++Index//為節點u設定次序編號和Low初值 Stack.push(u)//將節點u壓入棧中 for each(u,v) in E//枚舉每一條邊 if (visnotvisted)//如果節點v未被訪問過 tarjan(v)//繼續向下找 Low[u]=min(Low[u],Low[v]) else if (vinS)//如果節點v還在棧內 Low[u]=min(Low[u],DFN[v]) if (DFN[u]==Low[u])//如果節點u是強連通分量的根 repeat{ v=S.pop//將v退棧,為該強連通分量中一個頂點 printv until(u==v) }}pascal代碼
procedure tarjan(x:longint);var i,j,k:longint;begin inc(h); dfn[x]:=h;low[x]:=h;//dfn,low初始化,記錄訪問該點的真實時間dfn和最早時間low inc(t); f[t]:=x;//當前元素入棧 s[x]:=true;ss[x]:=true;//s,ss標記 for i:=1 to 200 do if p[x,i] then begin//枚舉每一條邊 if not s[i] then begin tarjan(i);//如果節點i未被訪問過繼續向下找 low[x]:=min(low[x],low[i]); end else if ss[i] then low[x]:=min(low[x],dfn[i]);//如果節點i還在棧內 end; if dfn[x]=low[x] then//如果s的最早訪問時間等於其實際訪問時間,則可把其視作迴路的"始點" begin inc(ans);//連通塊編號 while f[t+1]<>x do//將由x直接或間接擴展出的點標記為同一連通塊,標記訪問後出棧 begin ss[f[t]]:=false; dec(t); end; end;//如果節點x是強連通分量的根,退棧直到x的前一個數據,記錄這個強連通分量的數據end;
C++代碼
#define M 5010//題目中可能的最大點數int STACK[M],top=0;//Tarjan算法中的棧bool InStack[M];//檢查是否在棧中int DFN[M];//深度優先搜尋訪問次序int Low[M];//能追溯到的最早的次序int ComponentNumber=0;//有向圖強連通分量個數int Index=0;//索引號vector<int> Edge[M];//鄰接表表示vector<int> Component[M];//獲得強連通分量結果int InComponent[M];//記錄每個點在第幾號強連通分量里int ComponentDegree[M];//記錄每個強連通分量的度void Tarjan(int i){ int j; DFN[i]=Low[i]=Index++; InStack[i]=true;STACK[++top]=i; for (int e=0;e<Edge[i].size();e++) { j=Edge[i][e]; if (DFN[j]==-1) { Tarjan(j); Low[i]=min(Low[i],Low[j]); } else if (InStack[j]) Low[i]=min(Low[i],DFN[j]);//也可Low[i]=min(Low[i],Low[j]);僅限在求強聯通分量時 } if (DFN[i]==Low[i]) { ComponentNumber++; do{ j=STACK[top--]; InStack[j]=false; Component[ComponentNumber]. push_back(j); InComponent[j]=ComponentNumber; } while (j!=i); }}