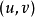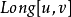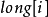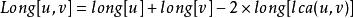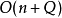LCA（Lowest Common Ancestors），即最近公共祖先，是指在有根樹中，找出某兩個結點u和v最近的公共祖先。
基本介紹
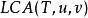
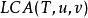
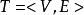
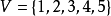
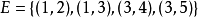
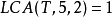
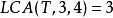
基本介紹,實現,重要結論,
基本介紹
LCA（Least Common Ancestors），即最近公共祖先，是指在有根樹中，找出某兩個結點u和v最近的公共祖先。
對於有根樹T的兩個結點u、v，最近公共祖先
表示一個結點x，滿足x是u、v的祖先且x的深度儘可能大。
另一種理解方式是把T理解為一個無向無環圖，而
即u到v的最短路上深度最小的點。
這裡給出一個LCA的例子：
對於
實現
暴力枚舉（樸素算法）
對於有根樹T的兩個結點u、v，首先將u，v中深度較深的那一個點向上蹦到和深度較淺的點，然後兩個點一起向上蹦，直到蹦到同一個點，這個點就是u，v的最近公共祖先，記作LCA（u，v）。
但是這種方法的時間複雜度在極端情況下會達到
。特別是有多組數據求解時，時間複雜度將會達到O（n*m）。
例：
在當這棵樹是二叉查找樹的情況下，如下圖：
那么從樹根開始：
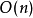
- 如果當前結點t 大於結點u、v，說明u、v都在t 的左側，所以它們的共同祖先必定在t 的左子樹中，故從t 的左子樹中繼續查找；
- 如果當前結點t 小於結點u、v，說明u、v都在t 的右側，所以它們的共同祖先必定在t 的右子樹中，故從t 的右子樹中繼續查找；
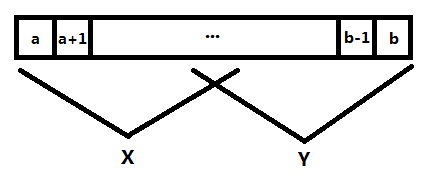
- 如果當前結點t 滿足 ，說明u和v分居在t 的兩側，故當前結點t 即為最近公共祖先；
- 而如果u是v的祖先，那么返回u的父結點，同理，如果v是u的祖先，那么返回v的父結點。
int query(Node t, Node u, Node v) { int left = u.value; int right = v.value; //二叉查找樹內，如果左結點大於右結點，不對，交換 if (left > right) { int temp = left; left = right; right = temp; } while (true) { //如果t小於u、v，往t的右子樹中查找 if (t.value < left) t = t.right; //如果t大於u、v，往t的左子樹中查找 else if (t.value > right) t = t.left; else return t.value; }}運用DFS序
DFS序就是用DFS方法遍歷整棵樹得到的序列。
兩個點的LCA一定是兩個點在DFS序中出現的位置之間深度最小的那個點，
尋找最小值可以使用RMQ。
複雜度參考值：
int tot, seq[N << 1], pos[N << 1], dep[N << 1];// dfs過程，預處理深度dep、dfs序數組seqvoid dfs(int now, int fa, int d) { pos[now] = ++tot, seq[tot] = now, dep[tot] = d; for (int i = head[now]; i; i = e[i].next) { int v = e[i].to; if (v == fa) continue; dfs(v, now, d + 1); seq[++tot] = now, dep[tot] = d; }}int anc[N << 1][20]; // anc[i][j]表示i節點向上跳2^j層對應的節點void init(int len) { for (int i = 1; i <= len; i++) anc[i][0] = i; for (int k = 1; (1 << k) <= len; k++) for (int i = 1; i + (1 << k) - 1 <= len; i++) if (dep[anc[i][k - 1]] < dep[anc[i + (1 << (k - 1))][k - 1]]) anc[i][k] = anc[i][k - 1]; else anc[i][k] = anc[i + (1 << (k - 1))][k - 1];}int rmq(int l, int r) { int k = log(r - l + 1) / log(2); return dep[anc[l][k]] < dep[anc[r + 1 - (1 << k)][k]] ? 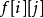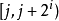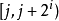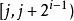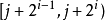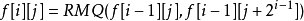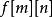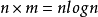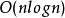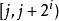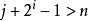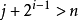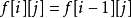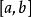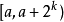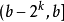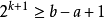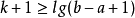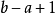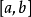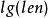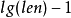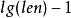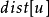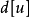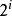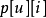anc[l][k] : anc[r + 1 - (1 << k)][k];}int calc(int x, int y) { x = pos[x], y = pos[y]; if (x > y) swap(x, y); return seq[rmq(x, y)];}int lca(int a, int b) { dfs(root, 0, 1); // root為樹根節點的編號 init(0); return calc(a, b);}倍增尋找（ST算法）
此算法基於動態規劃。
用
表示區間起點為j長度為2^i的區間內的最小值所在下標，通俗的說，就是區間
的區間內的最小值的下標。
從定義可知，這種表示法的區間長度一定是2的冪，所以除了單位區間(長度為1的區間)以外，任意一個區間都能夠分成兩份，並且同樣可以用這種表示法進行表示，
可以列出狀態轉移方程為：
。
原數組長度為n，當
區間右端點
時如何處理？在狀態轉移方程中只有一個地方會下標越界，所以當越界的時候狀態轉移只有一個方向，即當
時，
。
求解f[i][j]的代碼就不給出了，只需要兩層循環的狀態轉移就搞定了。
f[i][j]的計算只是做了一步預處理，但是我們在詢問的時候，不能保證每個詢問區間長度都是2的冪，如何利用預處理出來的值計算任何長度區間的值就是我們接下來要解決的問題。
首先只考慮區間長度大於1的情況（區間長度為1的情況最小值就等於它本身），給定任意區間
，必定可以找到兩個區間X和Y，它們的並是
，並且區間X的左端點是a，區間Y的右端點是b，而且兩個區間長度相當，且都是2的冪，如圖所示：
設區間長度為
，則X表示的區間為
，Y表示的區間為
，則需要滿足一個條件就是X的右端點必須大於等於Y的左端點減一，即
，則
, 兩邊取對數（以2為底），得
，則
，k只要需要取最小的滿足條件的整數即可( lg(x)代表以2為底x的對數 )。
仔細觀察發現
正好為區間
的長度len，所以只要區間長度一定，k就能在常數時間內求出來。而區間長度只有n種情況，所以k可以通過預處理進行預存。
當
為整數時，k 取
，否則k為
的上整（並且只有當len為2的冪時，
才為整數）。
我們注意到，在整個倍增查找LCA的過程中，從u到v的整條路徑都被掃描了一遍。如果我們在倍增數組F[i][j]中再記錄一些別的信息，就可以實現樹路徑信息的維護和查詢
實現過程：
預處理：通過dfs遍歷，記錄每個節點到根節點的距離
，深度
init()求出樹上每個節點u的
祖先
求最近公共祖先，根據兩個節點的的深度，如不同，向上調整深度大的節點，使得兩個節點在同一層上，如果正好是祖先結束，否則，將兩個節點同時上移，查詢最近公共祖先。
核心代碼如下：
void dfs(int u) { for(int i=head[u]; i!=-1; i=edge[i].next) { int to=edge[i].to; if(to==p[u][0])continue; d[to]=d[u]+1; dist[to]=dist[u]+edge[i].w; p[to][0]=u; //p[i][0]存i的父節點 dfs(to); }}void init()//i的2^j祖先就是i的（2^(j-1))祖先的2^(j-1)祖先{ for(int j=1; (1<<j)<=n; j++) for(int i=1; i<=n; i++) p[i][j]=p[p[i][j-1]][j-1];}int lca(int a,int b) { if(d[a]>d[b])swap(a,b); //b在下面 int f=d[b]-d[a]; //f是高度差 for(int i=0; (1<<i)<=f; i++) //(1<<i)&f找到f化為2進制後1的位置，移動到相應的位置 if((1<<i)&f)b=p[b][i]; //比如f=5，二進制就是101,所以首先移動2^0祖先，然後再移動2^2祖先 if(a!=b) { for(int i=(int)log2(N); i>=0; i--) if(p[a][i]!=p[b][i]) //從最大祖先開始，判斷a,b祖先，是否相同 a=p[a][i], b=p[b][i]; //如不相同，a b同時向上移動2^j a=p[a][0]; //這時a的father就是LCA } return a;}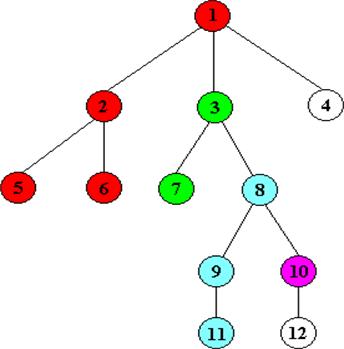ST算法可以擴展到二維，用四維的數組來保存狀態，每個狀態表示的是一個矩形區域中的最值，可以用來求解矩形區域內的最值問題。
Tarjan算法（離線算法）
離線算法，是指首先讀入所有的詢問（求一次LCA叫做一次詢問），然後重新組織查詢處理順序以便得到更高效的處理方法。Tarjan算法是一個常見的用於解決LCA問題的離線算法，它結合了深度優先遍歷和並查集，整個算法為線性處理時間。
同上一個算法一樣，Tarjan算法也要用到深度優先搜尋，算法大體流程如下：對於新搜尋到的一個結點，首先創建由這個結點構成的集合，再對當前結點的每一個子樹進行搜尋，每搜尋完一棵子樹，則可確定子樹內的LCA詢問都已解決。其他的LCA詢問的結果必然在這個子樹之外，這時把子樹所形成的集合與當前結點的集合合併，並將當前結點設為這個集合的祖先。之後繼續搜尋下一棵子樹，直到當前結點的所有子樹搜尋完。這時把當前結點也設為已被檢查過的，同時可以處理有關當前結點的LCA詢問，如果有一個從當前結點到結點v的詢問，且v已被檢查過，則由於進行的是深度優先搜尋，當前結點與v的最近公共祖先一定還沒有被檢查，而這個最近公共祖先的包涵v的子樹一定已經搜尋過了，那么這個最近公共祖先一定是v所在集合的祖先。
如圖：
根據實現算法可以看出，只有當某一棵子樹全部遍歷處理完成後，才將該子樹的根節點標記為黑色（初始化是白色），假設程式按上面的樹形結構進行遍歷，首先從節點1開始，然後遞歸處理根為2的子樹，當子樹2處理完畢後，節點2， 5， 6均為黑色；接著要回溯處理3子樹，首先被染黑的是節點7（因為節點7作為葉子不用深搜，直接處理），接著節點7就會查看所有詢問(7, x)的節點對，假如存在(7, 5)，因為節點5已經被染黑，所以就可以斷定(7, 5)的最近公共祖先就是find(5).ancestor，即節點1（因為2子樹處理完畢後，子樹2和節點1進行了union，find(5)返回了合併後的樹的根1，此時樹根的ancestor的值就是1）。有人會問如果沒有(7, 5)，而是有(5, 7)詢問對怎么處理呢? 我們可以在程式初始化的時候做個技巧，將詢問對(a, b)和(b, a)全部存儲，這樣就能保證完整性。
參考代碼如下：
const int mx = 10000; //最大頂點數int n, root; //實際頂點個數，樹根節點int indeg[mx]; //頂點入度，用來判斷樹根vector<int> tree[mx]; //樹的鄰接表（不一定是二叉樹）void inputTree() //輸入樹{ scanf("%d", &n); //樹的頂點數 for (int i = 0; i < n; i++) //初始化樹，頂點編號從0開始 tree[i].clear(), indeg[i] = 0; for (int i = 1; i < n; i++) //輸入n-1條樹邊 { int x, y; scanf("%d%d", &x, &y); //x->y有一條邊 tree[x].push_back(y); indeg[y]++;//加入鄰接表，y入度加一 } for (int i = 0; i < n; i++) //尋找樹根，入度為0的頂點 if (indeg[i] == 0) { root = i; break; }}vector<int> query[mx]; //所有查詢的內容void inputQuires() //輸入查詢{ for (int i = 0; i < n; i++) //清空上次查詢 query[i].clear(); int m; scanf("%d", &m); //查詢個數 while (m--) { int u, v; scanf("%d%d", &u, &v); //查詢u和v的LCA query[u].push_back(v); query[v].push_back(u); }}int father[mx], rnk[mx]; //節點的父親、秩void makeSet() //初始化並查集{ for (int i = 0; i < n; i++) father[i] = i, rnk[i] = 0;}int findSet(int x) //查找{ if (x != father[x]) father[x] = findSet(father[x]); return father[x];}void unionSet(int x, int y) //合併{ x = findSet(x), y = findSet(y); if (x == y) return; if (rnk[x] > rnk[y]) father[y] = x; else father[x] = y, rnk[y] += rnk[x] == rnk[y];}int ancestor[mx]; //已訪問節點集合的祖先bool vs[mx]; //訪問標誌void Tarjan(int x) //Tarjan算法求解LCA{ for (int i = 0; i < tree[x].size(); i++) { Tarjan(tree[x][i]); //訪問子樹 unionSet(x, tree[x][i]); //將子樹節點與根節點x的集合合併 ancestor[findSet(x)] = x;//合併後的集合的祖先為x } vs[x] = 1; //標記為已訪問 for (int i = 0; i < query[x].size(); i++) //與根節點x有關的查詢 if (vs[query[x][i]]) //如果查詢的另一個節點已訪問，則輸出結果 printf("%d和%d的最近公共祖先為：%d\n", x, query[x][i], ancestor[findSet(query[x][i])]);}int main(){ inputTree(); //輸入樹 inputQuires();//輸入查詢 makeSet(); for (int i = 0; i < n; i++) ancestor[i] = i; memset(vs, 0, sizeof(vs)); //初始化為未訪問 Tarjan(root);}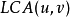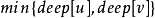樹鏈剖分
對於輸入的這棵樹，先對其進行樹鏈剖分處理。顯然，樹中任意點對(u,v)只存在兩種情況：
1. 兩點在同一條重鏈上。
2. 兩點不在同一條重鏈上。
對於1，
明顯為u,v兩點中深度較小的點，即
。
對於2，我們只要想辦法將u,v兩點轉移到同一條重鏈上即可。
所以，我們可以將u,v一直上調，每次將u,v調至重鏈頂端，直到u,v兩點在同一條重鏈上即可。
核心代碼如下
const int N=500004;int head[N*2],next[N*2],to[N*2];// 樹的鄰接表int deep[N],fa[N];// deep表示節點深度，fa表示節點的父親int size[N],son[N],top[N];// size表示節點所在的子樹的節點總數 // son表示節點的重孩子 // top表示節點所在的重鏈的頂部節點inline void add(int u,int v,int tnt)// 鄰接表加邊{ nt[tnt]=ft[u]; ft[u]=tnt; ed[tnt]=v;}void DFS(int u,int Fa)// 第一遍dfs，處理出deep，size，fa，son{ size[u]=1; for(int i=head[u];i;i=next[i]) { if(to[i]==Fa) continue; deep[to[i]]=d[u]+1; fa[to[i]]=u; DFS(to[i],u); size[u]+=size[to[i]]; if(size[to[i]]>size[son[u]]) son[u]=to[i]; }}void Dfs(int u)// 第二遍dfs，將所有相鄰的重邊連成重鏈{ if(u==son[fa[u]]) top[u]=top[fa[u]]; else top[u]=u; for(int i=head[u];i;i=next[i]) if(to[i]!=fa[u]) Dfs(to[i]);}int LCA(int u,int v)// 處理LCA{ while(top[u]!=top[v])// 如果u,v不在同一條重鏈上 { if(deep[top[u]]>deep[top[v]])// 將深度大的節點上調 u=fa[top[u]]; else v=fa[top[v]]; } return deep[u]>deep[v]?v:u;// 返回深度小的節點（即為LCA(u,v)）}附並查集介紹
講個簡單的故事來加深對並查集的理解，這個故事要追溯到北宋年間。話說北宋時期，朝綱敗壞，奸臣當道，民不聊生。又有外侮遼軍大舉南下，於是眾多能人異士群起而反，各大武林門派同仇敵愾，共抗遼賊，為首的自然是中原武林第一大幫-丐幫，其幫主乃萬軍叢中取上將首級猶如探囊取物、泰山崩於前而面不改色的北喬峰；與其齊名的是空有一腔抱負、壯志未酬的南慕容帶領的慕容世家；當然也少不了天下武功的鼻祖-少林，以及一些小幫派，如逍遙派、靈鷲宮、無量劍、神農教等等。我們將每個門派（幫派）作為一個集合，從中選出一個代表作為這個集合的標識，姑且認為門派（幫派）的掌門（幫主）就是這個代表。
作者有幸成了“抗遼聯盟”的統計員，統計員只有一個工作，就是接收一條條同門數據，然後統計共有多少個門派，好進行分派部署。同門數據的格式為(x, y)，表示x和y屬於同一個門派，接收到一條數據，需要對x所在的群體和y的群體進行合併，當統計完所有數據後有多少個集合就代表多少個門派。
這個問題其實隱含了兩個操作：1、查找a和b是否已經在同一個門派；2、如果兩個人的門派不一致，則合併這兩個人所在集合的兩堆人。分別對應了並查集的查找和合併操作。
如圖所示，分別表示丐幫、少林、逍遙、大理段氏四個集合。
重要結論
若樹上兩點
的路徑長度為
，
則
