基本介紹
- 中文名:有向圖
- 外文名:oriented graph
- 類型:表示物件與物件之間的關係
- 三元組:V(D),A(D),ψD
相關概念
鄰接矩陣

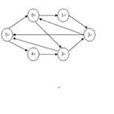

一個有向圖D是指一個有序三元組(V(D),A(D),ψD),其中ψD)為關聯函式,它使A(D)中的每一個元素(稱為有向邊或弧)對應於V(D)中的一個有序元素(稱...
有向完全圖是指圖中各邊都有方向,且每兩個頂點之間都有兩條方向相反的邊連線的圖。...... 有向完全圖是指圖中各邊都有方向,且每兩個頂點之間都有兩條方向...
有向無環圖指的是一個無迴路的有向圖。如果有一個非有向無環圖,且A點出發向B經C可回到A,形成一個環。將從C到A的邊方向改為從A到C,則變成有向無環圖...
歐拉有向圖(Eulerian digraph)一種特殊的強連通有向圖.若一個有向圖D上存在一條有向閉徑C,使得D的每一條弧都在C上,則稱D為歐拉有向圖.這種閉徑被稱為有...
有向樹也許是圖論中使用最廣泛的一類圖形,特別是在計算機科學中資料庫的構造以及語言的編譯方面用途極廣。在根樹T中,出度為零的點稱為樹葉,T中其他頂點稱為內...
《有向圖的理論算法及其套用》作者從近30年關於有向圖理論研究的數千篇論文中精選了具有理論意義、重要算法及其實際套用的結果,涵蓋了有向圖理論中從最基本到較為...
邊沒有方向的圖稱為無向圖。...... (3)若G是無向圖,則0≤e≤n(n-1)/2恰有n(n-1)/2條邊的無向圖稱無向完全圖(Undirected Complete Graph)...
美國加州大學伯克利分校的克里斯托斯·帕帕迪米特里歐(Christos Papadimitriou) 教授定義了PPAD(polynomial parity arguments on directed graphs,有向圖的多項式校驗參數)...
一般來說,圖可分為有向圖和無向圖。有向圖的所有邊都有方向,即確定了頂點到頂點的一個指向;而無向圖的所有邊都是雙向的,即無向邊所連線的兩個頂點可以互相...
強連通圖(Strongly Connected Graph)是指在有向圖G中,如果對於每一對vi、vj,vi≠vj,從vi到vj和從vj到vi都存在路徑,則稱G是強連通圖。有向圖中的極大強...
入度是圖論算法中重要的概念之一。它通常指有向圖中某點作為圖中邊的終點的次數之和。...
因此,用一個一維數組存放圖中所有頂點數據;用一個二維數組存放頂點間關係(邊或弧)的數據,這個二維數組稱為鄰接矩陣。鄰接矩陣又分為有向圖鄰接矩陣和無向圖鄰接...
設G=(V,E)是有向圖,對於任意u,v∈V,從u可達v或者從v可達u,則稱G為單向連通圖(unilateral connected digraph)。...
在圖論中,連通圖基於連通的概念。在一個無向圖 G 中,若從頂點i到頂點j有路徑相連(當然從j到i也一定有路徑),則稱i和j是連通的。如果 G 是有向圖,那么...
在有向圖中,為圖中每個頂點vi建立一個入邊表的方法稱逆鄰接表表示法。入邊表中的每個表結點均對應一條以vi為終點(即射入vi)的邊。...
在無向圖中,關聯一對頂點的無向邊如果多於1條,則稱這些邊為平行邊,平行邊的條數稱為重數。在有向圖中,關聯一對頂點的有向邊如果多於1條,並且這些邊的始點...
在圖論中,連通圖基於連通的概念。在一個無向圖G中,若從頂點到頂點有路徑相連(當然從到也一定有路徑),則稱和是連通的。如果G是有向圖,那么連線和的路徑中所有...
若從中選擇n-1條邊,使得無向圖仍然連通,則由n個頂點及這 n-1條邊(弧)組成的圖被稱為原無向圖的生成樹。中文名 圖 外文名 Graph 學科 數學 分類 有/...
在圖論的數學領域,完全圖是一個簡單的無向圖,其中每對不同的頂點之間都恰連有一條邊相連。完整的有向圖又是一個有向圖,其中每對不同的頂點通過一對唯一的...
無向圖的鄰接矩陣一定是對稱的,而有向圖的鄰接矩陣不一定對稱。因此,用鄰接矩陣來表示一個具有n個頂點的有向圖時需要n^2個單元來存儲鄰接矩陣;對有n個頂點的...
一個無向圖存在歐拉迴路,若且唯若該圖所有頂點度數都為偶數,且該圖是連通圖。有向圖存在歐拉迴路的充要條件一個有向圖存在歐拉迴路,所有頂點的入度等於出度且...
在無向圖中,關聯一對頂點的無向邊如果多於1條,則稱這些邊為平行邊,平行邊的條數稱為重數。在有向圖中,關聯一對頂點的有向邊如果多於1條,並且這些邊的始點...
