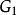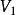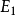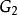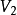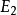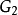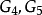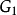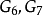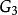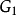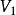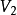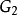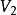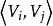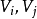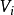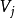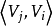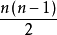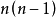一般來說,圖可分為有向圖和無向圖。有向圖的所有邊都有方向,即確定了頂點到頂點的一個指向;而無向圖的所有邊都是雙向的,即無向邊所連線的兩個頂點可以互相到達。在一些問題中,可以把無向圖當作所有邊都是正向和負向的兩條有向邊組成。頂點的度是指和該頂點相連的邊的條數。特別是對於有向圖來說,頂點的出邊條數稱為該頂點的出度,頂點的入邊條數稱為該項點的入度。
基本介紹
- 中文名:出度
- 外文名:out-degree
- 所屬學科:數據結構
- 相關概念:有向圖、度、出度等
基本介紹,相關概念,圖的定義,子圖,
基本介紹
1" style="float: none; display: block; margin: 0px auto; clear: both;" picsrc="dc54564e9258d1095aa22d4cda58ccbf6d814d8f" data-layout="blockcenter" width="158" height="142" url="https://gss1.bdstatic.com/9vo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=2293c7c74036acaf5de091fe4cd88d03/dc54564e9258d1095aa22d4cda58ccbf6d814d8f.jpg" compressw="158" compressh="142" useredit="1" />

2" style="float: none; display: block; margin: 0px auto; clear: both;" picsrc="7aec54e736d12f2e0419219e44c2d56285356834" data-layout="blockcenter" width="206" height="183" url="https://gss1.bdstatic.com/-vo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=dd789fe3df2a283447a631096bb4c92e/7aec54e736d12f2e0419219e44c2d56285356834.jpg" compressw="206" compressh="183" useredit="1" />

設無向圖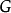 有
有 個頂點,e條邊,每個頂點的度為
個頂點,e條邊,每個頂點的度為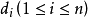 ,則有:
,則有:
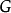

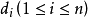
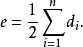
相關概念
圖的定義
一個圖由一個非空有限頂點集和一個邊的有限集組成。圖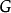 的頂點集和邊集分別用
的頂點集和邊集分別用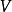 和
和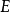 表示,則圖G可表示成
表示,則圖G可表示成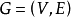 。
。
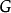
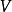
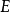
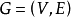
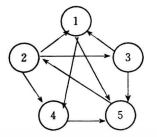 圖1(a) G1 |  圖1(b) G2 |  圖1(c) G3 |
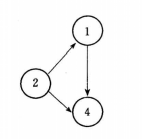 圖1(d)G4 |  圖1(d) G5 | 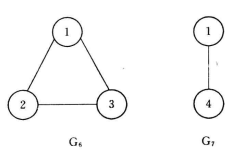 圖1(d) G6、G7 |
子圖
設圖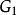 的頂點集和邊集為
的頂點集和邊集為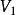 和
和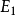 ,圖
,圖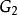 的頂點集和邊集為
的頂點集和邊集為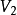 和
和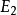 ,若:
,若: