基本介紹
- 中文名:接合函式
- 外文名:incidence function
- 別稱:關聯函式
- 所屬學科:數學(組合序)
- 簡介:一類映射
基本介紹,接合代數,相關介紹,
基本介紹
接合函式是一類映射,即從局部有限偏序集P=(E,≤)的笛卡兒積集P×P,到數域F上且滿足如下條件的映射f:當E的任意元素x,y沒有序關係,即x≰y時,f(x,y)=0。
從組合幾何觀點看,x,y沒有序關係也就是沒有接合關係。
例如,δ函式δ(x,y)僅當x=y時其值為1,其他情形均為0;ζ函式ζ(x,y)僅當x≤y時其值為1,而其他情形均為0。
接合代數
若AF(p)為如前所述所有接合函式組成的集合,並在其上定義接合函式的加法運算、數乘運算以及卷積運算:
(f+g)(x,y)=f(x,y)+g(x,y);
(rf)(x,y)=rf(x,y),r∈F;
(f*g)(x,y)=f(x,z)g(z,y),
則稱AF(P)為P的接合代數。而且它關於偏序集P是惟一的,不僅如此,當不同的偏序集P1,P2產生的接合代數AF(P1)和AF(P2)同構時,偏序集P1和P2亦同構。
相關介紹
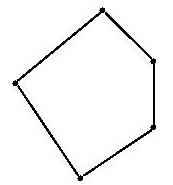
偏序集(partially set,poset)是特定的集,它是一類主要的序關係集。具體地說,集合E連同其上的偏序R構成的關係集(E,R),一般記為P=(E,≤)。所謂偏序(或序關係)是一類具有自反性、反對稱性和傳遞性的二元關係。例如,數之間的不大於關係,自然數之間的整除關係,集合之間的包容關係等。把集合E的基數稱為偏序集P的階,階為有限值的偏序集稱為有限偏序集。而在P上,對於任意元素x,y,區間[x,y]均為有限偏序集時,稱P為局部有限偏序集,這兩類偏序集是組合理論中的主要研究對象。偏序集上所有鏈的長度的最小上界,或上確界,稱為偏序集的長度,記為l(P),偏序集中最大反鏈包含的元素數目,稱為偏序集的寬度,記w(p),對於以下圖為哈塞圖的偏序集P,有l(P)=3,w(P)=2,偏序集的子關係集仍為偏序集,而且必有全序集作為其子關係集。
在集合P上定義一個二元關係≤,對任意x,y,z∈P,若滿足下列條件:
P1x≤x(反身性);
P2若x≤y且y≤x,則x=y(反對稱性);
P3若x≤y且y≤z,則x≤z(傳遞性),
則稱P為偏序集,記為(P;≤),或簡記為P,滿足P1,P2,P3的二元關係稱為偏序關係,簡稱偏序,亦稱半序.集合P的二元關係 適合P1,P3時,稱為擬序或準序,記為(P;
適合P1,P3時,稱為擬序或準序,記為(P; ),並稱其為擬序集或準序集.若(P;≤)是偏序集,Q是P的一個非空子集,而且在Q上有一個由≤引出的自然偏序≤Q,使對a,b∈Q,a≤Qb若且唯若a≤b,則稱(Q;≤Q)為P的子偏序集.設≤1,≤2是定義在同一集合P上的兩個偏序,對任意a,b∈P,若a≤1b有a≤2b,則≤2稱為≤1的擴張.當x≤y且x≠y時,則稱x小於y,亦稱x真含於y,並記為x<y,關係x≤y亦可寫成y≥x,讀成y含x(或包括x),(P;≤)和(P;≥)稱為對偶的偏序集。
),並稱其為擬序集或準序集.若(P;≤)是偏序集,Q是P的一個非空子集,而且在Q上有一個由≤引出的自然偏序≤Q,使對a,b∈Q,a≤Qb若且唯若a≤b,則稱(Q;≤Q)為P的子偏序集.設≤1,≤2是定義在同一集合P上的兩個偏序,對任意a,b∈P,若a≤1b有a≤2b,則≤2稱為≤1的擴張.當x≤y且x≠y時,則稱x小於y,亦稱x真含於y,並記為x<y,關係x≤y亦可寫成y≥x,讀成y含x(或包括x),(P;≤)和(P;≥)稱為對偶的偏序集。



