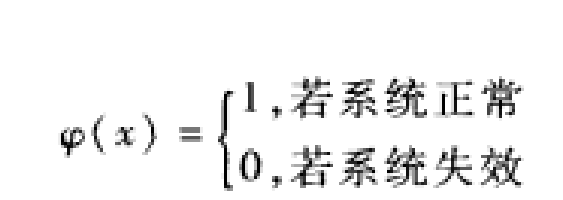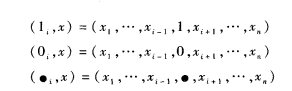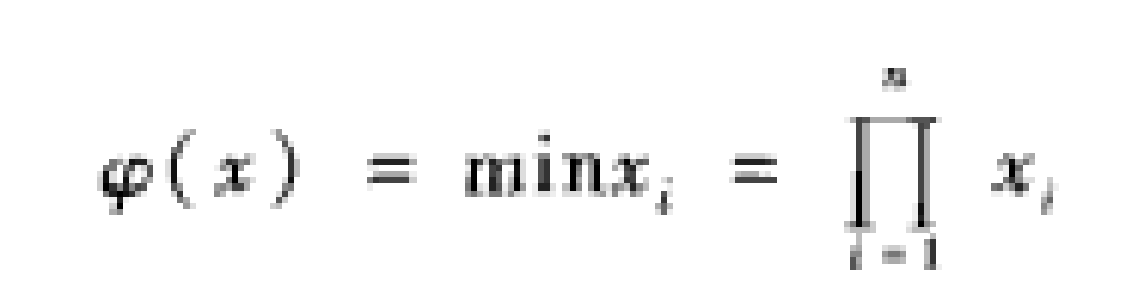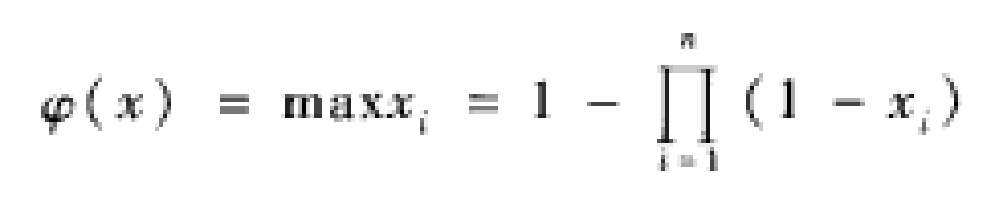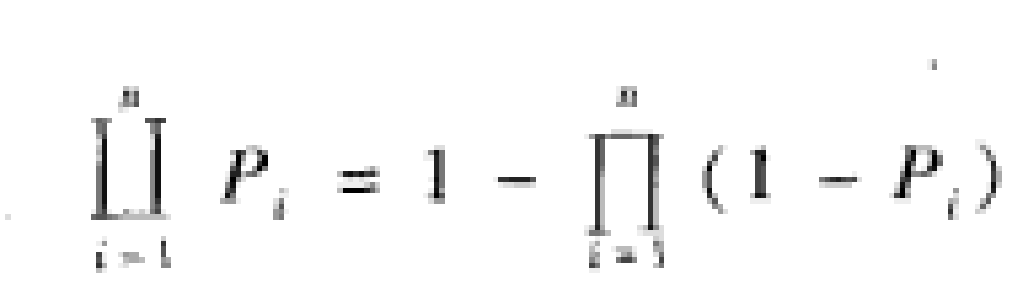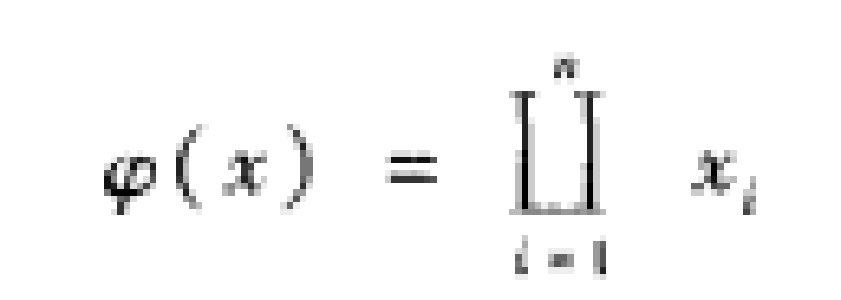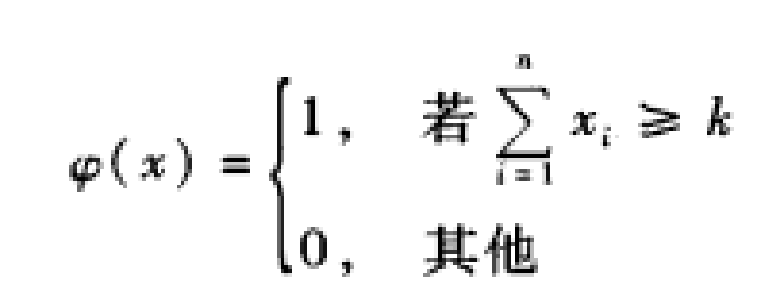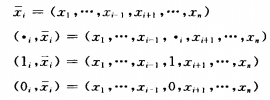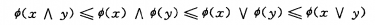結構函式有單調性的一類系統.設系統由n個部件組成,相應的結構函式為φ.此系統為關聯繫統.如果它的結構函式φ滿足（"ni"表示“n”的下標為“i”）:
1.單調性.即ᗄx≤y,有φ(x)≤φ(y).這裡x≤y表示分量間有xi≤yi (i=1,2,…,n). 2.部件與系統的可靠性有關係.即對任意i (1≤i≤n),存在x使
0=φ(0i,x)<φ(1i,x)=1,
這裡(0i,x),(1i,x)分別表示x中第i個分量取0或1時的狀態向量. 直觀上講,結構函式的單調性反映了用性能好的部件組成的系統,比用差的部件組成的系統的性能要好;第二個條件說明,每個部件對系統的可靠性都是有貢獻的,因而在可靠性意義下是不可少的.許多典型系統,如(k/n)(F)系統、網路系統等都是關聯繫統的特例.
單調關聯繫統，簡稱關聯繫統。
基本介紹
- 中文名：關聯繫統
- 外文名：coherent system
- 別名：單調關聯繫統
- 相關概念：結構函式
- 所屬學科：數理科學
詳細介紹,性質,
詳細介紹
假定系統由n個部件組成。若所有部件只有正常和失效兩狀態，令
用x=(x1,x2,......,xn)表示部件狀態向量。假定系統亦只有正常和失效兩狀態，且系統正常與否完全由系統的結構和部件的狀態所決定。這樣，對給定的部件狀態向量x，系統的狀態可表示為
則稱φ(x)為系統的結構函式。
定義1 設P是系統的結構函式，若對任意的：x≤y有
φ(x)<φ(y)
則稱φ是單調結構函式，或單調系統，記作φ∈{MS}。顯然，單調結構函式反映了部件狀態的改善不會使系統變壞。進一步，引入
記號
定義2 若對某個部件i，存在x使φ(0i,x)=0,φ(1i,x)=1，則稱部件i與系統有關。
上述性質稱為部件與系統的關聯性。反之，若某個部件i，對所有x都有φ(0i,x)<φ(1i,x)，則部件i與系統無關，即不論部件i是好還是壞(xi=l或xi=0)，在任何情況下對系統都沒有影響。從可靠性的角度來看，無關部件對系統不起任何作用。
定義3 若系統具有單調結構函式φ，且系統中的所有部件都與系統有關，則稱系統為單調關聯繫統，記作φ(∈{CS}。
n個部件的串聯繫統是單調關聯繫統，其結構函式為
並聯繫統也是單凋關聯繫統，其結構函式為
在可靠性理論中常用下列特別的記號：對任意的0≤pi≤1(i=1,2,......,n)，有
因此並聯繫統的結構函式可表示為
k/n(G)表決系統的結構函式是
如果每個部件都與系統有關，但系統是非單調系統，則稱系統為非單調關聯繫統。在實踐中遇到的大多數系統是單調關聯繫統。至於非單調關聯繫統有時也會見到，例如在帶反饋的自動控制系統中經常會出現這類系統。
如果認為結構函式是關於系統和單元的可靠性的一種表示方式，那么它自然應具有以下性質。
(1)Φ(1)=1，Φ(0)=0。
(2)若x≥y(定義為xi≥yi，i=1，2，…，n)，則Φ(x)≥Φ(y)。
性質(1)表明，所有單元都工作時系統也工作，所有單元都發生故障時系統也發生故障；性質(2)則表示當某些失效單元恢復工作而其他單元的狀態保持不變時，系統不可能變得更差。例如，有一系統滿足
Φ(1,0,1)=0 ; Φ(1,0,1)=1(1,0,1)≥(1,0,1)
該系統就不滿足性質(2)。但這恰恰說明了這樣的反常狀態：由於重新工作的單元3發生了故障，系統從故障狀態回到了工作狀態。性質(2)排除了這種反常狀況。這意味著，當系統處於故障狀態時，由於工作單元發生故障，系統不會恢復到工作狀態；相反，也不會出現當系統工作時，由於故障單元恢復工作狀態而系統故障。具有性質(2)的結構函式稱為單調結構函式，因為函式Φ具有單調性。對應的系統稱為單調系統。
引入如下記號
對結構函式Φ(x)，如果對所有的
均有Φ(1i, )=Φ(0i, )
則稱單元i為無關單元(因為它對系統正常與否無任何影響)。不包含無關單元的單調系統稱為單調關聯繫統，簡稱關聯繫統。顯然，單調系統中如有無關單元，則只要去掉全部無關單元，剩下部分組成的系統必是單調關聯繫統。
性質
可以證明，單調關聯繫統具有概論中的性質(1)和性質(2)之外，還具有如下兩條性質。
1.
2.對x=(x1，x2，…，xn)，y=(y1，y2，…，yn)，若記x∧≤y=(x1∧y1，x2∧y2，…，
xn∧yn)，x∨y=(x1∨y1，x2∨y2，…，xn∨yn)，則
上述的性質(3)說明在所有的單調關聯繫統的結構函式中，串聯繫統的結構函式是最小的，而並聯繫統的結構函式是最大的。性質(4)則進一步說明了結構函式妒的單調性。
