含有平行邊的圖稱為多重圖。也稱若圖中某兩個結點之間的邊數多於一條,又允許頂點通過同一條邊和自己關聯,則稱為多重圖。多重圖的定義和簡單圖是相對的。
基本介紹
- 中文名:多重圖
- 外文名:multigraph
- 定義:含平行邊的圖稱為多重圖
- 相關概念:有向圖、無向圖、平行邊等
定義
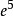
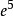


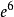
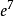
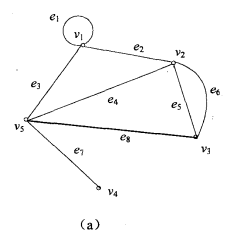 圖1(a)
圖1(a)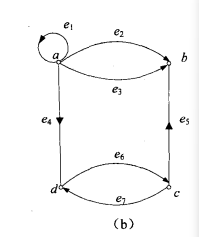 t圖1(b)
t圖1(b)基礎概念

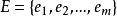
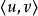
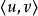
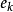
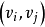
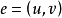
多重圖的矩陣表示
有向多重圖
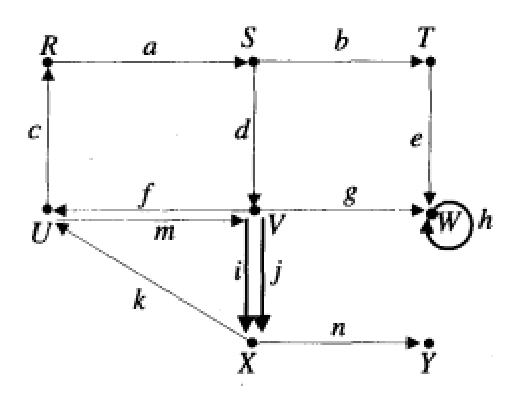
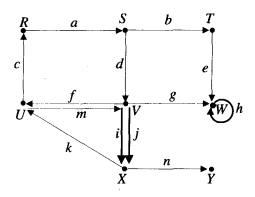 圖2
圖2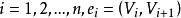
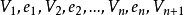
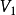
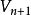
含有平行邊的圖稱為多重圖。也稱若圖中某兩個結點之間的邊數多於一條,又允許頂點通過同一條邊和自己關聯,則稱為多重圖。多重圖的定義和簡單圖是相對的。
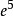
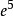


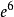
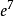
 圖1(a)
圖1(a) t圖1(b)
t圖1(b)
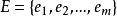
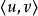
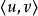
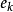
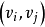
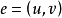
 圖2
圖2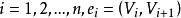
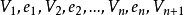
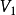
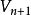
含有平行邊的圖稱為多重圖。也稱若圖中某兩個結點之間的邊數多於一條,又允許頂點通過同一條邊和自己關聯,則稱為多重圖。多重圖的定義和簡單圖是相對的。...
半導體多重圖形製造法(Semiconductor multi-pattern manufacturing method)是指一種在半導體製造過程中的技術。在光刻過程中使用了多重圖形曝光增強了製作圖形的密度。...
多重網路圖形,Multiple-image Network Graphics(MNG)是多幀PNG動畫圖形格式,功能類似GIF。目前多數主流瀏覽器均不直接支持MNG。...
鄰接多重表是無向圖的一種存儲方式。鄰接多重表是鄰接表的改進,它把邊的兩個頂點存放在邊表結點中,所有依附於同一個頂點的邊串聯在同一鍊表中,由於每條邊依附...
第2-4章介紹限制圖譜和多重圖譜,第5、6章研究克隆和克隆圖譜,第7章討論DNA...3.2.6 限制圖譜及邊界塊圖3.2.7 限制圖譜的盒變換3.2.8 一個例子問題...
曝光補償 ±5EV(1/3EV步長)(運動圖片±3EV) ±5EV(1/3EV步長)(運動圖片...其它曝光性能 測光系統:1728 區域多重圖樣感測系統 測光範圍:EV 0-18(F2.0 鏡...
±3EV(用於運動圖片) ±3EV(使用撥盤設定時 ±5EV(1/3EV步長) ±3EV(用於運動圖片) ±3EV(使用撥盤設定時 測光方式 多重測光,中央重點測光,點測光 多重...
網頁 新聞 貼吧 知道 音樂 圖片 視頻 地圖 文庫 百科 進入詞條全站搜尋幫助 ...第2-4章介紹限制圖譜和多重圖譜,第5、6章研究克隆和克隆圖譜,第7章討論DNA...
