連通圖

在圖論中，連通圖基於連通的概念。在一個無向圖 G 中，若從頂點i到頂點j有路徑相連（當然從j到i也一定有路徑），則稱i和j是連通的。如果 G 是有向圖，那么連線i和j的路徑中所有的邊都必須同向。如果圖中任意兩點都是連通的，那么圖被稱作連通圖。如果此圖是有向圖，則稱為強連通圖（注意：需要雙向都有路徑）。圖的連通性是圖的基本性質。

基本介紹

• 中文名：連通圖
• 外文名：connected graph
• 學科：數學，計算機
• 所屬領域：圖論
• 性質：連通性
• 相關術語：無向圖 

嚴格定義

對一個圖G= (V,E)中的兩點x和y，若存在交替的頂點和邊的序列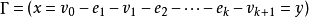（在有向圖中要求有向邊屬於E），則兩點 x和y是連通的。是一條x到y的連通路徑，x和y分別是起點和終點。當x=y時，被稱為迴路。如果通路中的邊兩兩不同，則是一條簡單通路，否則為一條複雜通路。如果圖G中每兩點間皆連通，則G是連通圖。

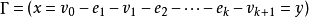
相關概念

連通分量：無向圖 G的一個極大連通子圖稱為 G的一個連通分量（或連通分支）。連通圖只有一個連通分量，即其自身；非連通的無向圖有多個連通分量。

強連通圖：有向圖 G=(V,E) 中，若對於V中任意兩個不同的頂點 x和 y，都存在從x到 y以及從 y到 x的路徑，則稱 G是強連通圖。相應地有強連通分量的概念。強連通圖只有一個強連通分量，即是其自身；非強連通的有向圖有多個強連分量。

單向連通圖：設G=<V,E>是有向圖，如果u->v意味著圖G至多包含一條從u到v的簡單路徑，則圖G為單連通圖。

弱連通圖：將有向圖的所有的有向邊替換為無向邊，所得到的圖稱為原圖的基圖。如果一個有向圖的基圖是連通圖，則有向圖是弱連通圖。

初級通路：通路中所有的頂點互不相同。初級通路必為簡單通路，但反之不真。

性質

一個無向圖 G=(V,E) 是連通的，那么邊的數目大於等於頂點的數目減一：|E|>=|V|-1，而反之不成立。

如果 G=(V,E) 是有向圖，那么它是強連通圖的必要條件是邊的數目大於等於頂點的數目：|E|>=|V|，而反之不成立。

沒有迴路的無向圖是連通的若且唯若它是樹，即等價於：|E|=|V|-1。