kosaraju算法

在計算機科學中，Kosaraju的算法（也稱為Kosaraju-Sharir算法）是線性時間的算法來找到一個有向圖的強連通分量。

Aho, Hopcroft 和Ullman相信這個算法是由S. Rao Kosaraju在1978在一個未發表的論文上提出的。

相同的算法還從Micha Sharir 1981年自己出版的書上被單獨的發現，這個算法利用了一個事實，即轉置圖（同圖中的每邊的方向相反）具有和原圖完全一樣的強連通分量。

基本介紹

• 中文名：Kosaraju算法
• 外文名：Kosaraju's algorithm
• 提出者：S. Rao Kosaraju
• 提出時間：1978
• 套用學科：計算機科學
• 適用領域範圍：圖論 ACM編程

算法思想

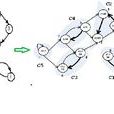
Kosaraju算法的解釋和實現都比較簡單，為了找到強連通分支，首先對圖G運行DFS，計算出各頂點完成搜尋的時間f；然後計算圖的逆圖GT，對逆圖也進行DFS搜尋，但是這裡搜尋時頂點的訪問次序不是按照頂點標號的大小，而是按照各頂點f值由大到小的順序；逆圖DFS所得到的森林即對應連通區域。具體流程如圖(1~4)。

上面我們提及原圖G的逆圖GT，其定義為GT=(V,ET)，ET={(u,v):(v,u)∈E}}。也就是說GT是由G中的邊反向所組成的，通常也稱之為圖G的轉置。在這裡值得一提的是，逆圖GT和原圖G有著完全相同的連通分支，也就說，如果頂點s和t在G中是互達的，若且唯若s和t在GT中也是互達的。

為了方便大家理解，附下引用部落格中的例圖：

原圖

原圖進行dfs

上面是第一次dfs

逆圖

逆圖dfs，獲得強連通分量

這裡對逆圖進行dfs，就可以得到強連通分量了。

偽代碼

1. 對原圖G進行深度優先遍歷，記錄每個節點的離開時間num[i]
2. 選擇具有最晚離開時間的頂點，對反圖GT進行遍歷，刪除能夠遍歷到的頂點，這些頂點構成一個強連通分量
3. 如果還有頂點沒有刪除，繼續步驟2，否則算法結束

c++代碼

#include <bits/stdc++.h> /* Kosaraju求強連通分量鄰接矩陣 */ using namespace std; int map[511][511];int nmap[511][511];int visited[501];stack<int>S;int N;int DFS1(int  v) /* visitedthevnode */{    visited[v] = 1;    for (int i = 1;i <= N;i++)        if (!visited[i] && map[v][i])            DFS1( i );    S.push( v );    return 0;}int DFS2( int v ){    visited[v] = 1;    for (int i = 1;i <= N;i++)        if ( !visited[i] && nmap[v][i] )            DFS2( i );    return 0;}int kosaraju(){    while (!S.empty())        S.pop();    memset(visited,0,sizeof(visited));    for (int i = 1;i <= N;i++)        if (!visited[i]) DFS1( i );    int t = 0;    memset(visited,0,sizeof(visited));    while (!S.empty())    {        int v = S.top();        S.pop();        print f( "|%d|", v );        if (!visited[v])        {            t++;            DFS2( v );        }    }    return t;}int main(){    int M,s,e;    scanf("%d%d",&N,&M);    memset(map,0,sizeof(map) );    memset(nmap,0,sizeof(nmap) );    for (int i = 0; i < M; i++)    {        scanf("%d%d",&s,&e);        map[s][e] = 1;        nmap[e][s] = 1;    }    printf("%d\n", kosaraju()); /* 輸出連通分量個數 */    return0;}

551221233441

樣例輸出：

2