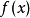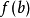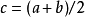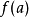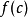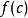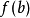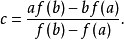在數學和電腦運算中，對於一個已知的從實數集合映射到實數集合，或者從複數集合映射到複數集合的連續函式f(x)，搜尋變數x使得f(x)=0（此時，變數x稱為f(x)=0的根、f(x)的零點）的算法，稱為求根算法。在許多情況下，函式的零點無法被準確計算出，也無法被解析解表示；是故，求根算法在實數集合下只提供一個以浮點數表示的近似解，或者一個足夠小的解的存在區間，在複數集合下只提供一個復根的圓盤（輸出一個區間或一個圓盤等價於輸出一個根的近似值及其誤差上限）。
解方程f(x)=g(x)與求f(x)-g(x)的根是等價的。因此求根算法可以求解任何以連續函式定義的方程。然而，許多情況下，求根算法只能找到方程的某些根，而不能保證所有根都能找到；特別指出，算法未找到根，並不代表方程確實無根。
基本介紹
- 中文名：求根法
- 外文名：Root-finding algorithm
- 學科：數學
- 性質：數學方法
- 用於：因式分解
簡介,包圍法,二分法,盈不足術法,插值法,疊代法,牛頓法（及類似的以導數為基礎的方法）,割線法,逆插值法,
簡介
大多數的數值求根算法都使用疊代法，生成一個以方程的根為極限的收斂數列。它們需要一個或多個根作為疊代的初期值，嗣後每次疊代都生成一個逐步逼近根的值。由於疊代法必須在有限步內終止於某個點，這些方法都只能提供一個根的近似值，而不能提供一個精確解。 許多方法是通過代入上一個疊代值來計算一個輔助方程，從而得出下一個疊代值的。此處所指的輔助方程是指為了使源方程的根是一個定點並使疊代值能更快地收斂到這些定點而設計的一個方程，因此疊代值的極限是這個輔助方程的一個定點。
求根算法的性能是數值分析的研究範疇。一種算法的效率可能大幅度取決於已知點的性質。例如，一部分算法都使用輸入函式的導數（此要求函式不但連續，而且可導），而其他算法則能用於任何一個連續函式。在一般情況下，數值算法不能保證找到一個函式的所有根，因此算法未能找到根並不能證明方程無根。然而，對於多項式，存在特定的使用代數學性質以定位根的所在區間（或復根所在的圓盤）的算法，這個區間（或圓盤）足夠小以能保證數值算法（例如牛頓法）能收斂到唯一被定位的根。
包圍法
包圍法是指通過疊代確定根的所在區間，並逐漸縮小其區間長度的算法。當區間變得足夠小時，則認為根已經被找到。一般地，包圍法以介值定理為基礎，且能夠求出根的絕對誤差上限；而當函式是一個多項式時，還有其它基於施圖姆定理或笛卡兒符號法則的方法，能夠在一個區間內求出精確的根。
二分法
最簡單的求根算法為二分法︰令
為一個連續函式，且已知存在區間
滿足
和
符號互異。令
（區間的中點），則
和
或
和
中，必恰有一者符號互異，並將已知根所在區間的長度縮短為一半。對被縮短的區間重複上述步驟，直到找到根。
縱二分法具有強健性，但其只能求得區間內的一個且只有一位精度的解。此外在合適的條件下，亦存在其他能更快求得精確解的方法。
盈不足術法
盈不足術法與二分法相似。異處在於，盈不足術以方式計算出疊代點，
盈不足術法也類似於割線法。異處在於，盈不足術法不保留前兩次疊代點，而是在根的兩側各保留一點。 盈不足術法能以較二分法更快的速度求根，且不會如割線法一樣發散（不收斂）；但在一些簡單實現的情形中可能因為捨入誤差而無法收斂。
Ridders法是盈不足術法的一個變形。其使用區間中點的函式值，構造出一個具有相同零點的函式，再用盈不足術法求解之。這個方法維持了一定的強健性外，亦使算法更快收斂。
插值法
疊代法
雖然所有求根算法都通過疊代，但一個疊代的求根算法，通常使用一種特定的疊代類型，包括定義一個輔助函式，套用上一步計算出的根的近似值，求得新的近似值。輔助函式到逹一個定點（到逹所需的精度），即新疊代的近似值充分接近上一個疊代值時，疊代停止。
牛頓法（及類似的以導數為基礎的方法）
牛頓法假定函式
的導數是連續的。如果起始點距離根太遠，牛頓法可能不收斂。然而，其若收斂，速度將較二分法快，且通常為二次收斂。牛頓法也是一種重要的算法，因為它能容易地推廣到高維問題。類似牛頓法且有更高次的收斂性的算法為Householder法。具有三次收斂性的Householder法是Halley法。
割線法
逆插值法
對函式
進行逆插值，能夠避免插值法中出現複數。這種方法稱為逆二次插值法。其收斂速度漸近快於割線法；但當疊代離根較遠時，逆二次插值法往往表現不佳。
