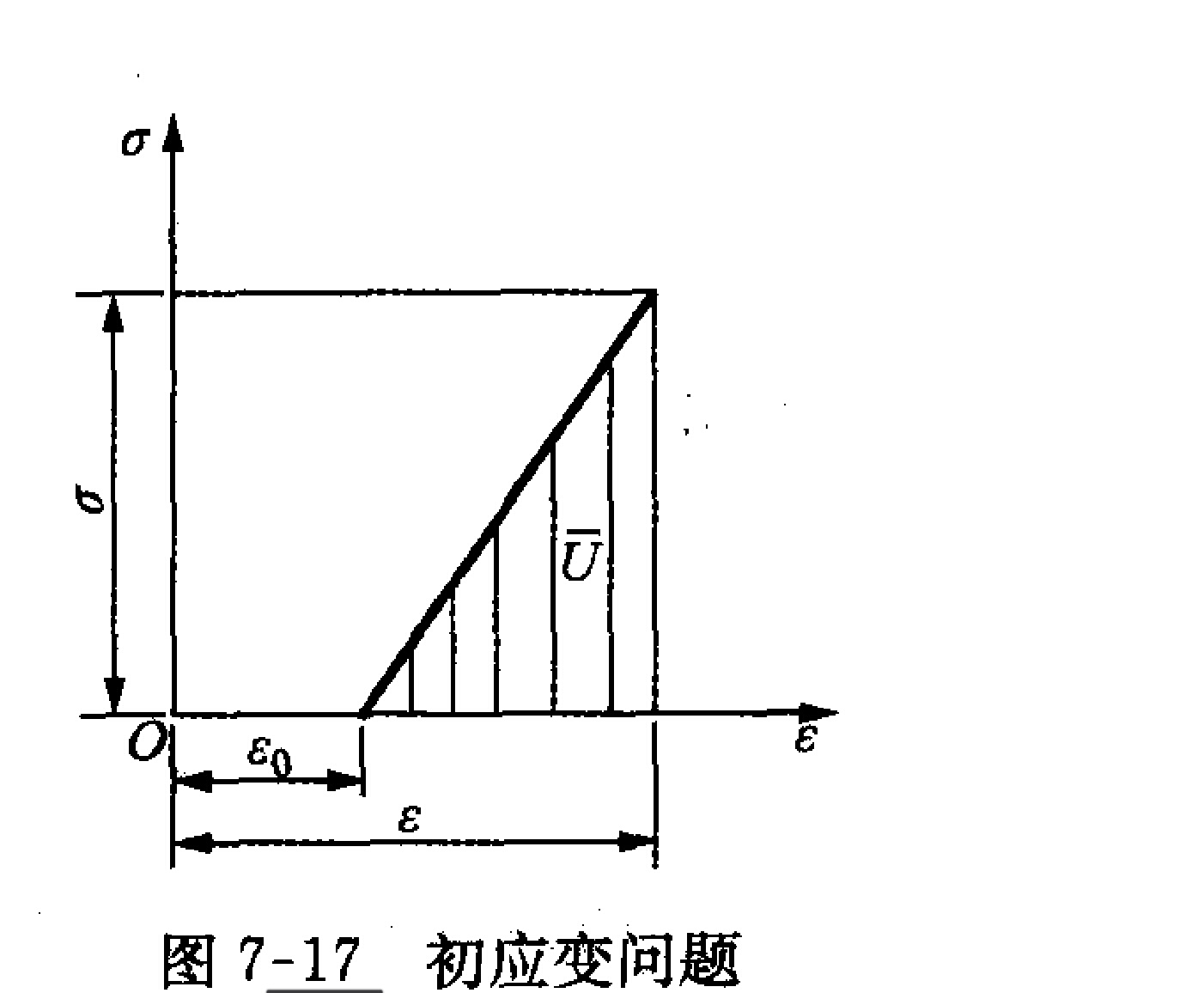
初應變法是一種進行有限元求解的求解方法。
具體原理如下:假設單元存在著初始應變{εo},應力-應變關係可以寫成:{σ}=[D]({ε}-{εo});
在有限元中,該單元相應的節點力為:{F}=∫∫[B]'[D][B]dxdy{δ}e+∫∫[B]'{D}{εo}dxdy=[k]{U}e+{Fo}e;
{Fo}e為初應變對應的節點力。
基本介紹
- 中文名:初應變法
- 外文名:Initial strain method
- 求解方法:進行有限元求解
- 具體原理 :Fo}e為初應變對應的節點力
- 理論發展:[K]{δ}={R}-{Ro}
- 套用學科:力學術語
概念,計算原理,缺陷,
概念
對具有初應變的彈性問題,其應力應變關係是:
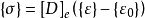

其中 為初應變數,它由元素初應變向量
為初應變數,它由元素初應變向量

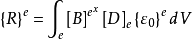
按有關的貢獻疊加而成。
類似的,我們可把彈塑性應力應變關係寫成:
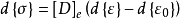
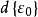
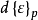
計算原理
對於整個有限元體系,可以從上式集成為:[K]{δ}={R}-{Ro}
上式表明:如果存在初應變,形成的有限元方程中僅僅是在荷載項中增加了一項。
根據這一原理,有限非線性分析中可以將非線性的應力-應變關係變化為:{σ}=[D]({ε}-{εo})。其中:{ε}為總應變,{εo}則為塑性應變。
具體計算過程如下:
1,先令{Ro}=0,通過荷載平衡解出第一次的位移近似解,及應變、應力近似解,通過非線性的本構關係和應力確定的應變解,該應變解與近似解之差,即為{εo}。然後按照上述的原理中的方法,即可得到增加的荷載項{R1},以此類推。
缺陷
初應變法的優點是收斂速度快,尤其是與餘量疊代法聯合使用時。但是,其缺點是當應力水平較高時(尤其是應力-應變曲線接近水平時)。計算穩定性太差。