平行弦法有兩種義項，一個是指一種非線性方程的數值解法，是一種疊代法，指用斜率不變的直線近似曲線得到疊代序列的求根方法，另一個是指平行於坐標面的圓的軸測圖的畫法。
基本介紹
- 中文名：平行弦法
- 外文名：parallel-chord method
- 所屬學科：數學
- 相關問題：弦截法，圓軸測圖的畫法等
非線性方程的數值解法,圓的軸測圖的畫法,
非線性方程的數值解法
平行弦法(parallel-chord method)是一種疊代法，指用斜率不變的直線近似曲線得到疊代序列的求根方法。用牛頓法及割線法求根時，每步疊代用直線近似曲線其直線斜率都在變化，為簡化計算，若逼近
的直線斜率c保持不變，直線取為
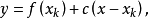
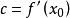
圓的軸測圖的畫法
平行弦法，就是通過平行於坐標軸的弦來定出圓周上的點，然後作出這些點的軸測投影，光滑連線以求得橢圓。
用平行弦法來求作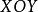
坐標面上圓的正二測軸測圖，如表1 (a)所示。
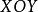
作圖：
(1)設立坐標體系，作軸測軸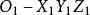
，如表1 (b)所示，取簡化軸向伸縮係數
；
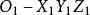
(2)用平行於OX軸的弦EF分割圓O，得分點E、R；
(3)求出點A、B、C、D、E、F的軸測投影
，如表1(c)所示，利用上述平行弦可求出圓周上一系列點的軸測投影；
(4)光滑連線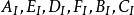
各點，得到圓O的正二測軸測圖，見表1(d)。
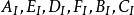
平行弦法不僅可用於平行於坐標面的圓的軸測圖的求作，也可用於不平行於坐標面的圓的軸測圖的求作。
